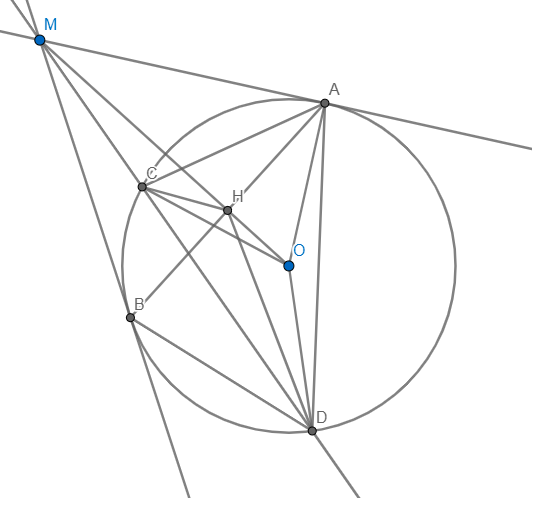
Từ điểm M nằm ngoài đường tròn (O), vẽ tiếp tuyến MA và MB và cát tuyến MCD. a) cm: MA²=MB²=MC.MD b) cm: AC.BD=AD.BC
(Cần gấp câu b ạ, mình cảm ơn)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AT
15 tháng 7 2021
ACBD nội tiếp \(\Rightarrow\angle ACD=\angle ABD=\angle HBD\)
Xét \(\Delta MAC\) và \(\Delta MDA:\) Ta có: \(\left\{{}\begin{matrix}\angle MAC=\angle MDA\\\angle DMAchung\end{matrix}\right.\)
\(\Rightarrow\Delta MAC\sim\Delta MDA\left(g-g\right)\Rightarrow\dfrac{MA}{MD}=\dfrac{MC}{MA}\Rightarrow MA^2=MC.MD\)
Vì MA,MB là tiếp tuyến \(\Rightarrow\Delta MAB\) cân tại M có MO là phân giác \(\angle AMB\)
\(\Rightarrow MO\bot AB\)
tam giác MAO vuông tại A có AH là đường cao \(\Rightarrow MA^2=MH.MO\)
\(\Rightarrow MH.MO=MC.MD\Rightarrow\dfrac{MH}{MD}=\dfrac{MC}{MO}\)
Xét \(\Delta MHC\) và \(\Delta MDO:\) Ta có: \(\left\{{}\begin{matrix}\dfrac{MH}{MD}=\dfrac{MC}{MO}\\\angle DMOchung\end{matrix}\right.\)
\(\Rightarrow\Delta MHC\sim\Delta MDO\left(c-g-c\right)\Rightarrow\angle MHC=\angle MDO\Rightarrow CHOD\) nội tiếp
Ta có: \(\angle BHD=90-\angle DHO=90-\angle DCO\) (CHOD nội tiếp)
\(=90-\dfrac{180-\angle COD}{2}=90-90+\dfrac{1}{2}\angle COD=\angle CAD\)
Xét \(\Delta BHD\) và \(\Delta CAD:\) Ta có: \(\left\{{}\begin{matrix}\angle CAD=\angle BHD\\\angle ACD=\angle HBD\end{matrix}\right.\)
\(\Rightarrow\Delta BHD\sim\Delta CAD\left(g-g\right)\Rightarrow\dfrac{BH}{CA}=\dfrac{BD}{CD}\Rightarrow BH.CD=BD.CA\)
25 tháng 5 2022
a: Xét tứ giác MAOB có \(\widehat{MAO}+\widehat{MBO}=180^0\)
nên MAOB là tứ giác nội tiếp(1)
Xét tứ giác OHMB có \(\widehat{OHM}+\widehat{OBM}=180^0\)
nên OHMB là tứ giác nội tiếp(2)
Từ (1) và (2) suy ra O,H,A,M,B cùng thuộc đường tròn
b: Xét ΔMAC và ΔMDA có
\(\widehat{MAC}=\widehat{MDA}\)
\(\widehat{AMC}\) chung
Do đó:ΔMAC\(\sim\)ΔMDA
Suy ra: MA/MD=MC/MA
hay \(MA^2=MD\cdot MC=MO^2-R^2\)
19 tháng 3 2022
1, Vì MA ; MB lần lượt là tiếp tuyến (O) với A;B là tiếp điểm
=> ^MAO = ^MBO = 900
Xét tam giác MAOB có ^MAO + ^MBO = 1800
mà 2 góc đối Vậy tứ giác MAOB là tứ giác nt 1 đường tròn
2, Xét tam giác MAC và tam giác MDA
^M _ chung
^MAC = ^MDA ( cùng chắn cung AC )
Vậy tam giác MAC ~ tam giác MDA (g.g)
\(\dfrac{MA}{MD}=\dfrac{MC}{MA}\Rightarrow MA^2=MD.MC\)
3, Ta có AM = MB ( tc tiếp tuyến cắt nhau )
OB = OA = R
Vậy MO là đường trung trực
Xét tam giác MAO vuông tại A, đường cao AH
AO^2 = OH . OM ( hệ thức lượng )
\(\Rightarrow OM.OH+MC.MD=AO^2+AM^2=OM^2\left(pytago\right)\)