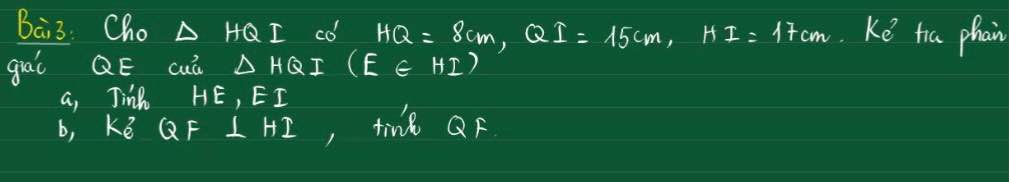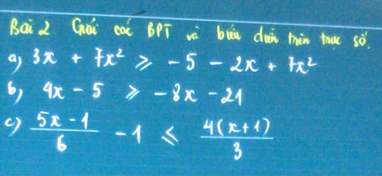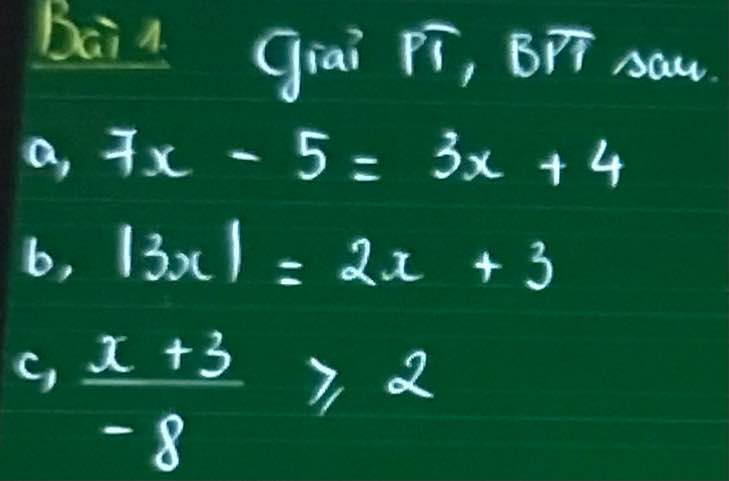các ac giúp e với ạ e xin cảm ơn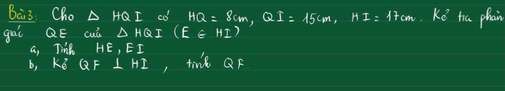 
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
6 tháng 3 2022
a) Xét tam giác HQI:
QE là phân giác \(\widehat{Q}\left(gt\right).\)
\(\Rightarrow\dfrac{HE}{EI}=\dfrac{HQ}{QI}\) (Tính chất phân giác).
\(\Rightarrow\dfrac{HE}{EI+HE}=\dfrac{HQ}{QI+HQ}.\)
\(\Rightarrow\dfrac{HE}{HI}=\dfrac{HQ}{QI+HQ}.\)
Thay: \(\dfrac{HE}{17}=\dfrac{8}{15+8}.\)
\(\Rightarrow HE=\dfrac{136}{23}\left(cm\right).\\ \Rightarrow EI=\dfrac{255}{23}\left(cm\right).\)
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 3 2023
\(A=\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^9}\)
\(\Rightarrow2A=1+\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^8}\)
\(\Rightarrow2A-A=1-\dfrac{1}{2^9}\)
\(\Rightarrow A=1-\dfrac{1}{2^9}=\dfrac{511}{512}\)
\(\Rightarrow\left(a+b\right)_{min}=511+512=1023\)
NL
1
18 tháng 2 2022
Câu 1.
a.Áp dụng tính chất đường phân giác, ta có:
\(\dfrac{AB}{AH}=\dfrac{BC}{CH}\)
\(\Leftrightarrow\dfrac{6}{8}=\dfrac{BC}{CH}\)
\(\Leftrightarrow\dfrac{CH}{8}=\dfrac{BC}{6}\)
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\dfrac{CH+BC}{8+6}=\dfrac{10}{14}=\dfrac{5}{7}\)
\(CH=\dfrac{5}{7}.8=\dfrac{40}{7}\)
\(BC=\dfrac{5}{7}.6=\dfrac{30}{7}\)
b.\(\Delta ABH\) là tam giác vuông vì:
\(HB^2=AB^2+AH^2\)
\(\Leftrightarrow10^2=6^2+8^2\) ( pitago đảo )
Áp dụng định lý pitago vào tam giác vuông ACB
\(AB^2=BC^2+AC^2\)
\(\Rightarrow AC=\sqrt{6^2-\dfrac{30}{7}^2}=\dfrac{12\sqrt{6}}{7}\)
\(S_{ABC}=\dfrac{1}{2}.BC.AC=\dfrac{1}{2}.\dfrac{30}{7}.\dfrac{12\sqrt{6}}{7}\simeq8,998cm^2\)
\(S_{ACH}=\dfrac{1}{2}.HC.AC=\dfrac{1}{2}.\dfrac{40}{7}.\dfrac{12\sqrt{6}}{7}\simeq11,997cm^2\)
NL
2
18 tháng 2 2022
Xét ΔABC có BD là phân giác
nên AB/AD=BC/CD
=>AB/4=BC/5
Đặt AB/4=BC/5=k
=>AB=4k; BC=5k
Theo đề, ta có: \(AB^2+AC^2=BC^2\)
\(\Leftrightarrow9k^2=81\)
=>k=3
=>AB=12; BC=15
18 tháng 2 2022
Vì BD là phân giác của \(\widehat{ABC}\) nên \(\dfrac{AD}{AB}=\dfrac{DC}{BC}\Leftrightarrow\dfrac{4}{AB}=\dfrac{5}{BC}\Leftrightarrow BC=\dfrac{5AB}{4}\)
Có : AC=AD+DC=4+5=9cm
Xét \(\Delta ABC\) vuông tại A có :
\(AB^2+AC^2=BC^2\) ( định lí Pi-ta-go)
\(AB^2+81=\dfrac{25AB^2}{16}\)
\(81=\dfrac{25AB^2}{16}-\dfrac{16AB^2}{16}\)
\(\Leftrightarrow\dfrac{9AB^2}{16}=81\)
\(9AB^2=1296\)
\(AB^2=144\)
AB=12 cm
Có : \(BC=\dfrac{5AB}{4}=\dfrac{5.12}{4}=15cm\)
NL
1
18 tháng 2 2022
a:Xét ΔAMN có MB là tia phân giác
nên AB/BN=AM/MN=AN/MN(1)
Xét ΔAMN có NC là tia phân giác
nên AC/CM=AN/MN(2)
Từ (1) và (2) suy ra AB/BN=AC/CM
hay BC//MN
b: Xét ΔCBM có \(\widehat{CBM}=\widehat{CMB}\)
nên ΔCBM cân tại C
=>CB=CM=6cm
Xét ΔABC có BC//MN
nên BC/MN=AC/AM
\(\Leftrightarrow\dfrac{AC}{AC+6}=\dfrac{1}{2}\)
=>AC=6(cm)
=>AM=12(cm)
NL
1
16 tháng 2 2022
a, \(3x+7x^2+5+2x-7x^2\ge0\Leftrightarrow5x+5\ge0\Leftrightarrow x\ge-1\)
b, \(12x\ge-16\Leftrightarrow x\ge-\dfrac{4}{3}\)
c, \(\dfrac{5x-1-6}{6}-\dfrac{4\left(x+1\right)}{3}\le0\)
\(\Leftrightarrow\dfrac{5x-7-8\left(x+1\right)}{6}\le0\Rightarrow-3x-15\le0\Leftrightarrow x\le-5\)
