CHo axbxc=1. Chứng minh:
A/ab+a+1 + b/bc+b+1 + 1/abc+bc+b=1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(a,\left\{{}\begin{matrix}MD=MB\\AM=MC\\\widehat{AMD}=\widehat{BMC}\left(đđ\right)\end{matrix}\right.\Rightarrow\Delta AMD=\Delta CMB\left(c.g.c\right)\\ \Rightarrow AD=BC\\ b,\Delta AMD=\Delta CMB\Rightarrow\widehat{MAD}=\widehat{MCB}\\ \text{Mà 2 góc này ở vị trí slt nên }AD\text{//}BC\\ c,\left\{{}\begin{matrix}NE=NC\\AN=NB\\\widehat{ANE}=\widehat{BNC}\left(đđ\right)\end{matrix}\right.\Rightarrow\Delta ANE=\Delta CNB\\ \Rightarrow AE=BC;\widehat{NAE}=\widehat{NCB}\Rightarrow AE\text{//}BC\left(\text{so le trong}\right)\\ \text{Mà }AD\text{//}BC\Rightarrow AD\equiv AE\text{ hay }A,D,E\text{ thẳng hàng}\\ \text{Mà }AE=AD\left(=BC\right)\\ \Rightarrow A\text{ là trung điểm }DE\)
a: Xét tứ giác ABCD có
M là trung điểm của AC
M là trung điểm của BD
Do đó: ABCD là hình bình hành
Suy ra: DA=BC

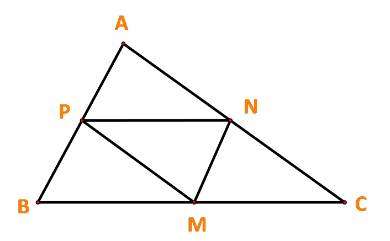
a) Ta có: \(\overrightarrow {BC} ,\overrightarrow {PN} \) là hai vecto cùng hướng và \(\frac{1}{2}\left| {\overrightarrow {BC} } \right| = \left| {\overrightarrow {PN} } \right|\)
\( \Rightarrow \frac{1}{2}\overrightarrow {BC} = \overrightarrow {PN} \)\( \Rightarrow \overrightarrow {AP} + \frac{1}{2}\overrightarrow {BC} = \overrightarrow {AP} + \overrightarrow {PN} = \overrightarrow {AN} \)
b) Ta có: \(\overrightarrow {MP} ,\overrightarrow {CA} \) là hai vecto cùng hướng và \(2\left| {\overrightarrow {MP} } \right| = \left| {\overrightarrow {CA} } \right|\)
\( \Rightarrow 2\overrightarrow {MP} = \overrightarrow {CA} \)\( \Rightarrow \overrightarrow {BC} + 2\overrightarrow {MP} = \overrightarrow {BC} + \overrightarrow {CA} = \overrightarrow {BA} \)

Ta có:
$\dfrac{1}{ab+a+1}+\dfrac{b}{bc+b+1}+\dfrac{1}{abc+bc+b}$
$=\dfrac{abc}{ab+a+abc}+\dfrac{b}{bc+b+1}+\dfrac{1}{1+bc+b}$ (do $abc=1$)
$=\dfrac{abc}{a(bc+b+1)}+\dfrac{b}{bc+b+1}+\dfrac{1}{1+bc+b}$
$=\dfrac{bc}{bc+b+1}+\dfrac{b}{bc+b+1}+\dfrac{1}{1+bc+b}$
$=\dfrac{bc+b+1}{bc+b+1}=1$
(đpcm)

Vì abc=1 nên:
\(\frac{1}{ab+a+1}+\frac{b}{bc+b+1}+\frac{1}{abc+bc+b}=\frac{1}{ab+a+1}+\frac{ab}{abc+ab+a}+\frac{a}{abc.a+abc+ab}=\frac{1}{ab+a+1}+\frac{ab}{1+ab+a}+\frac{a}{a+1+ab}=1\)
Chúc bạn học tốt.

a: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình
=>MN//BC và MN=1/2BC
b: Xét tứ giác AHCK có
N là trung điểm của AC
N là trung điểm của HK
Do đó: AHCK là hình bình hành
mà \(\widehat{AHC}=90^0\)
nên AHCK là hình chữ nhật
Suy ra: AC=HK