Phân tích thành phân tử 27x^3 - 1/8
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HH
2
19 tháng 7 2021
a) \(27x^3+27x^2+9x+1=\left(3x+1\right)^3\)
b) \(-x^3-3x^2-3x-1=-\left(x^3+3x^2+3x+1\right)=-\left(x+1\right)^3\)
c) \(-8+12x-6x^2+x^3=\left(x-2\right)^3\)
8 tháng 3 2017
\(8-27x^3=\left(2-3x\right)\left(4+6x+9x^2\right)\)
chắc đúng.thk cho mk
MH
17 tháng 10 2023
\(27x^3-27x^2+18x-4\)
\(=27x^3-9x^2-18x^2+6x+12x-4\)
\(=9x^2\left(3x-1\right)-6x\left(3x-1\right)+4\left(3x-1\right)\)
\(=\left(9x^2-6x+4\right)\left(3x-1\right)\)
LL
1
KT
30 tháng 7 2018
a) \(27x^3-8=\left(3x-2\right)\left(9x^2+6x+4\right)\)
b) \(8x^3+12x^2+6x+1=\left(2x+1\right)^3\)
c) \(\left(2y-1\right)^1-4x^2+4x-1=\left(2y-1\right)^2-\left(2x-1\right)^2=\left(2y-1-2x+1\right)\left(2y-1+2x-1\right)\)
\(=\left(2y-2x\right)\left(2y+2x-2\right)=4\left(y-x\right)\left(y+x-1\right)\)
T
26 tháng 8 2023
\(1-27x^3\)
\(=1-\left(3x\right)^3\)
\(=\left(1-3x\right)\left(1+3x+9x^2\right)\)
\(---\)
\(x-3^3+27\)
\(=x-27+27=x\)
\(---\)
\(27x^3+27x^2+9x+1\)
\(=\left(3x\right)^3+3\cdot\left(3x\right)^2\cdot1+3\cdot3x\cdot1^2+1^3\)
\(=\left(3x+1\right)^3\)
\(---\)
\(\dfrac{x^6}{27}-\dfrac{x^4y}{3}+x^2y^2-y^3\) (sửa đề)
\(=\left(\dfrac{x^2}{3}\right)^3-3\cdot\left(\dfrac{x^2}{3}\right)^2\cdot y+3\cdot\dfrac{x^2}{3}\cdot y^2-y^3\)
\(=\left(\dfrac{x^2}{3}-y\right)^3\)
#Ayumu
19 tháng 7 2021
a) \(x^3+9x^2+27x+27=\left(x+3\right)^3\)
b) \(3\sqrt{3x^3}+18x^2+12\sqrt{3x}+8=\left(\sqrt{3x}+2\right)^3\)
c) \(\dfrac{1}{4}-x^2=\left(\dfrac{1}{2}-x\right)\left(\dfrac{1}{2}+x\right)\)
MN
3
26 tháng 11 2016
\(8-27x^3\)
\(=2^3-\left(3x\right)^3\)
\(=\left(2-3x\right)\left(4+6x+9x^2\right)\)
26 tháng 11 2016
a) \(8-27x^3=\left(2-x\right)\left(4+6x+9x^2\right)\)
b) \(27+27x+9x^2+x^3=\left(3+x\right)^3\)
c) \(x^3+8y^3=\left(x+2y\right)\left(x^2-2xy+4y^2\right)\)
24 tháng 10 2020
\(1-27x^3\)
\(=1^3-\left(3x\right)^3\)
\(=\left(1-3x\right)\left(1+3x+9x^2\right)\)
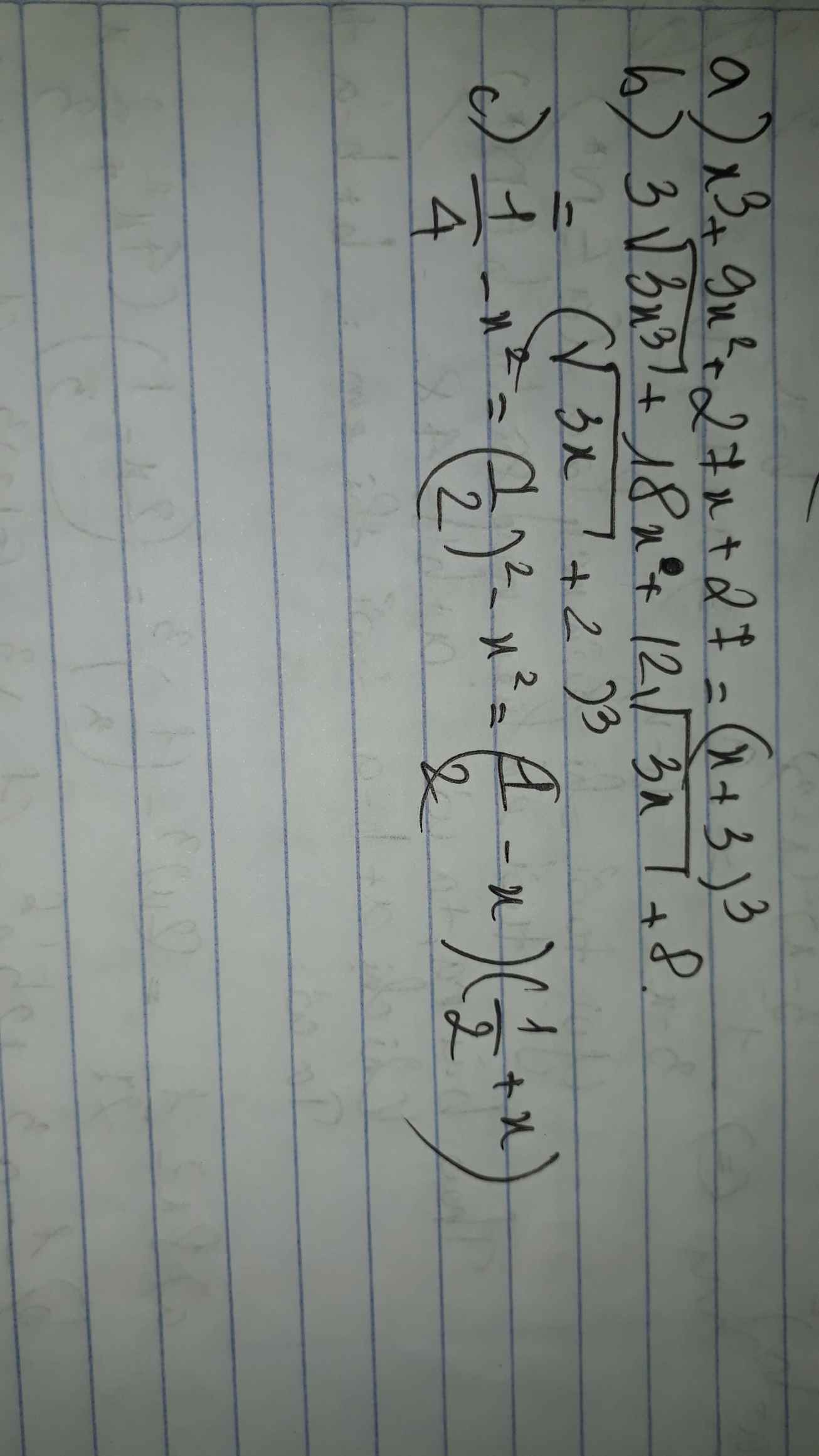
\(27x^3-\frac{1}{8}=\left(3x-\frac{1}{2}\right)\left(9x^2+\frac{3}{2}x+\frac{1}{4}\right)\)
(Nếu đúng thì click cho tớ với nhá!)
\(27x^3-\frac{1}{8}\)
\(=\left(3x\right)^3-\left(\frac{1}{2}\right)^3\)
\(=\left(3x-\frac{1}{2}\right)\left(9x^2+3x.\frac{1}{2}+\left(\frac{1}{2}\right)^2\right)\)
\(=\left(3x-\frac{1}{2}\right)\left(9x^2+\frac{3}{2}x+\frac{1}{4}\right)\)