mik cần ý b thôi ạ :,)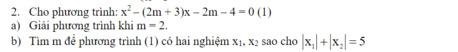
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
T
0
B
0
DT
giải nhanh giúp mik nha chỉ cần ý b vs ý d thôi
0
Y
28 tháng 9 2023
\(a,x=36\Leftrightarrow A=\dfrac{2+\sqrt{36}}{\sqrt{36}}=\dfrac{2+6}{6}=\dfrac{4}{3}\)
\(b,B=\dfrac{x}{x-4}-\dfrac{1}{2-\sqrt{x}}+\dfrac{1}{\sqrt{x}+2}\left(dkxd:x>0,x\ne4\right)\\ =\dfrac{x}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}+\dfrac{1}{\sqrt{x}-2}+\dfrac{1}{\sqrt{x}+2}\\ =\dfrac{x+\sqrt{x}+2+\sqrt{x}-2}{x-4}\\ =\dfrac{x+2\sqrt{x}}{x-4}\\ =\dfrac{\sqrt{x}\left(\sqrt{x}+2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\\ =\dfrac{\sqrt{x}}{\sqrt{x}-2}\)
\(c,P=\dfrac{A}{B}=\dfrac{2+\sqrt{x}}{\sqrt{x}}.\dfrac{\sqrt{x}-2}{\sqrt{x}}=\dfrac{x-4}{x}\)
Để \(Px\le\dfrac{3}{2}\left(\sqrt{x}-1\right)\) thì \(\dfrac{x-4}{x}.x\le\dfrac{3}{2}\left(\sqrt{x}-1\right)\)
\(\Leftrightarrow x-4-\dfrac{3}{2}\sqrt{x}+\dfrac{3}{2}\le0\\ \Leftrightarrow x-\dfrac{3}{2}\sqrt{x}-\dfrac{5}{2}\le0\)
\(\Leftrightarrow x\le\dfrac{25}{4}\)
Kết hợp với điều kiện \(x>0,x\ne4,x\in Z\), ta kết luận \(S=\left\{1;2;3;5;6\right\}\)
KC
3
25 tháng 1 2022
Đây ạ :
Bài thơ thể hiện sâu sắc tình cảnh đáng thương của ông đồ đúng không?
\(\Delta=\left(2m+3\right)^2+4\left(2m+4\right)=4m^2+20m+25=\left(2m+5\right)^2\ge0;\forall m\)
Pt đã cho luôn có 2 nghiệm với mọi m
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2m-3\\x_1x_2=-2m-4\end{matrix}\right.\)
\(\left|x_1\right|+\left|x_2\right|=5\Leftrightarrow x_1^2+x_2^2+2\left|x_1x_2\right|=25\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2+2\left|x_1x_2\right|=25\)
\(\Leftrightarrow\left(2m-3\right)^2+2\left(2m+4\right)+2\left|2m+4\right|=25\)
\(\Leftrightarrow4m^2-8m-8+4\left|m+2\right|=0\)
TH1: \(m\ge-2\)
\(\Rightarrow4m^2-8m-8+4\left(m+2\right)=0\)
\(\Leftrightarrow4m^2-4m=0\Rightarrow\left[{}\begin{matrix}m=0\\m=1\end{matrix}\right.\) (thỏa mãn)
TH2: \(m\le-2\)
\(\Rightarrow4m^2-8m-8-4\left(m+2\right)=0\)
\(\Leftrightarrow4m^2-12m-16=0\Rightarrow\left[{}\begin{matrix}m=-1\left(loại\right)\\m=4\left(loại\right)\end{matrix}\right.\)