Có số tự nhiên n nào thỏa mãn :n2-14n-256 là scp
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


biểu thức đã cho là số tự nhiên khi n^2+14n-256=a^2(a là số tự nhiên)
n^2+14n+49=a^2+49+256=a^2+305
(n+7)^2= a^2+305
vì n là số tự nhiên nên n+7 là số tự nhiên nên (n+7)^2 là số chính phương có dang b^2(b là số tự nhiên)
suy ra a^2+305=b^2
b^2-a^2=305
(b-a)(b+a)=305
vì a và b là số tự nhiên nên a+b là số tự nhiên và b+a>b-a
suy ra b+a là ước tự nhiên của 305={1;5;61;305}
nếu b+a=1 thì b-a=305>b+a(loại)
nếu b+a=5 thì b-a=61>b+a(loại)
nếu b+a=61 thì b-a=5 suy ra a=28 thay vào tìm được n=26
nếu b+a=305 thì b-a=1 suy ra a=152 thay vào tìm đươc n=146
vây n=26 hoặc n=146 tmđb

Đặt \(n^2-14n-256=a^2\)
\(\Leftrightarrow\left(n^2-14n+49\right)-a^2=305\)
\(\Leftrightarrow\left(n-7\right)^2-a^2=305\)
\(\Leftrightarrow\left(n-7+a\right)\left(n-7-a\right)=305=5\cdot61\)
Đến đây làm nốt đi.
Đặt \(G=n^2-14n-256=a^2\)(là số chính phương)
\(\Leftrightarrow n^2-14n+49-305=a^2\)
\(\Leftrightarrow\left(n-7\right)^2-305=a^2\)
\(\Leftrightarrow\left(n-7\right)^2-a^2=305\)
\(\Leftrightarrow\left(n+a-7\right)\left(n-a-7\right)=305=5.61\)
Mà \(n+a-7\ge n-a-7\)nên \(\hept{\begin{cases}n+a-7=61\\n-a-7=5\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}n+a=68\\n-a=12\end{cases}}\Leftrightarrow n=\frac{68+12}{2}=40\)
Vậy n = 40 thì \(G=n^2-14n-256\)là số chính phương



giả sử \(n^2+6n+3\) là SCP
Đặt \(n^2+6n+3=k^2\)
\(\Rightarrow\left(n^2+6n+9\right)-k^2-6=0\\ \Rightarrow\left(n+3\right)^2-k^2=6\\ \Rightarrow\left(n-k+3\right)\left(n+k+3\right)=6\)
Vì \(n\in N\Rightarrow\left\{{}\begin{matrix}n-k+3\in Z,n+k+3\in Z\\n-k+3< n+k+3\\n-k+3,n+k+3\inƯ\left(6\right)\end{matrix}\right.\)
rồi bạn lập bảng ra, tự lm tiếp nhé


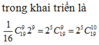
 Xài cái này gõ bài đi bạn, thề như này hiểu chết liền á :(
Xài cái này gõ bài đi bạn, thề như này hiểu chết liền á :(
Đề sai rồi hay sao ấy
\(n^2-14n-256=?\)
Sửa lại đi . Nếu đề đúng thì ko có n nào thỏa mãn