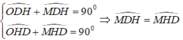Cho tam giác $ABC$ có ba góc nhọn ($AB < AC$), dựng $AH$ vuông góc với $BC$ tại $H$. Gọi $M$, $N$ theo thứ tự là hình chiếu vuông góc của điểm $H$ trên $AB$ và $AC$. Đường thẳng $MN$ cắt đường thẳng $BC$ tại điểm $D$. Trên nửa mặt phẳng bờ $CD$ chứa điểm $A$ vẽ nửa đường tròn đường kính $CD$. Qua $B$ kẻ đường thẳng vuông góc với $CD$ cắt nửa đường tròn trên tại điểm $E$.
a) Chứng minh tứ giác $AMHN$ là tứ giác nội tiếp.
b) Chứng minh \(\widehat{EBM}=\widehat{DNH}\).
c) Chứng minh $DM.DN = DB.DC$.