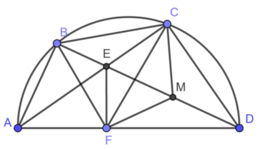
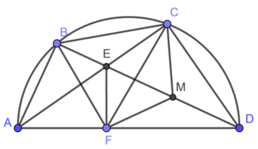
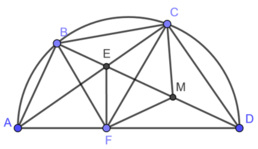
Cho tứ giác $ABCD$ nội tiếp đường tròn đường kính $AD$. Hai đường chéo $AC$ và $BD$ cắt nhau tại $E$. Gọi $F$ là điểm thuộc đường thẳng $AD$ sao cho $EF$ vuông góc với $AD$. Đường thẳng $CF$ cắt đường tròn đường kính $AD$ tại điểm thứ hai là $M$. Gọi $N$ là giao điểm của $BD$ và $CF$. Chứng minh rằng:
a) $CEFD$ nội tiếp đường tròn.
b) $FA$ là đường phân giác của góc $BFM$.
c) $BD.NE = BE.ND$.


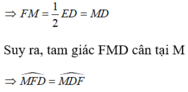
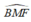 là góc ngoài tại đỉnh M của tam giác FMD nên:
là góc ngoài tại đỉnh M của tam giác FMD nên:
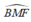 và
và 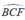 và cùng nhìn cạnh BF dưới một góc bằng nhau
và cùng nhìn cạnh BF dưới một góc bằng nhau