Cho tam giác $ABC$ không có góc tù $(AB < AC)$, nội tiếp đường tròn $(O; R)$, ($B$, $C$ cố định, $A$ di động trên cung lớn BC). Các tiếp tuyến tại $B$ và $C$ cắt nhau tại $M$. Từ $M$ kẻ đường thẳng song song với $AB$, đường thẳng này cắt $(O)$ tại $D$ và $E$ ($D$ thuộc cung nhỏ $BC$), cắt $BC$ tại $F$, cắt $AC$ tại $I$. Chứng minh rằng \(\widehat{MBC}=\widehat{BAC}\) . Từ đó suy ra $MBIC$ là tứ giác nội tiếp.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1)Cho tam giác nhọn ABC (AB<AC) nội tiếp đường tròn (O). Gọi H là trực tâm của tam giác ABC, K là giao điểm thứ hai của AH với đường tròn (O). Đường thẳng đi qua H và vuông góc với OA cắt BC ở I. Chứng minh rằng IK là tiếp tuyến của đường tròn (O)
~~~~~~~~~ Bài làm ~~~~~~~~~
A B C O I K H Q D
Ta có: \(\widehat{HBD}=\widehat{DAC}\) (Cùng phụ với \(\widehat{ACB}\))
\(\widehat{KBD}=\widehat{DAC}\)( Góc nối tiếp cùng chắn cung \(KC\))
\(\Rightarrow\widehat{HBD}=\widehat{KBD}\)
Ta lại có: \(BD\perp HK\)
\(\Rightarrow BD\) là đường trung trực của \(HK\)
\(\Rightarrow\Delta IHK\) cân tại \(I\)
\(\Rightarrow\widehat{BKD}=\widehat{BHD}=\widehat{AHQ}\)
Lại có:\(\widehat{DKO}=\widehat{HAO}\)( \(\Delta OKA\) cân tại \(O\))
Vì vậy: \(\widehat{DKO}+\widehat{BKD}=\widehat{HAO}+\widehat{AHQ}=90^0\)
\(\Rightarrow\widehat{KIO}=90^0\)
\(\Rightarrow IK\)là tiếp tuyến của đường tròn \(\left(O\right)\)
(Hình vẽ chỉ mang tính chất minh họa cái hình vẽ gần cả tiếng đồng hồ :)) )

Đáp án C
Tam giác ABC có góc A là góc tù nên 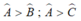
Mà cạnh đối diện với góc A là cạnh BC .
Áp dụng định lí: trong 1 tam giác cạnh đối diện với góc lớn hơn thì lớn hơn ta được:
BC > AC và BC > AB
Vậy tam giác ABC có độ dài cạnh BC là lớn nhất nên dây BC gần tâm nhất.
Chưa thể kết luận dây nào xa tâm nhất.

A B C D E O F
\(\widehat{\text{AFB}}=\widehat{ADB}=90^0\)
Mà ÀB và ADB là hai góc kề cùng nhìn AB dưới hai góc bằng nhau => ÀDB nội tiếp
b) ta có \(\widehat{ACB}=\widehat{AEB}\)( cùng chắn cung AB)
\(\widehat{DFC}=\widehat{BAF}\)( trong tứ giác nội tiếp góc ngaoif tại một đỉnh bằng góc trong đỉnh còn lại )
\(\Rightarrow\widehat{ACB}+\widehat{FDC}=\widehat{BAF}+\widehat{BAE}=90^0\)
\(\Rightarrow DF\perp CA\)

a)Xét tứ giác MBOC có
\(\widehat{OBM}\) và \(\widehat{OCM}\) là hai góc đối
\(\widehat{OBM}+\widehat{OCM}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: MBOC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)

a: góc BHD+góc BMD=180 độ
=>BHDM nội tiếp
b: BHDM nội tiếp
=>góc HDM+góc HBM=180 độ
=>góc ADM=góc ABC
=>góc ADM=góc ADC
=>DA là phân giáccủa góc MDC
c: Xét tứ giác DHNC có
góc DHC=góc DNC=90 độ
=>DHNC nội tiếp
=>góc NHD=góc NDC
góc NHD+góc MHD
=180 độ-góc NCD+góc MBD
=180 độ+180 độ-góc ABD-góc ACD
=180 độ
=>M,H,N thẳng hàng
Cho tam giác ABCABC không có góc tù (AB < AC)(AB<AC), nội tiếp đường tròn (O; R)(O;R), (BB, CC cố định, AA di động trên cung lớn BC). Các tiếp tuyến tại BB và CC cắt nhau tại MM. Từ MM kẻ đường thẳng song song với ABAB, đường thẳng này cắt (O)(O) tại DD và EE (DD thuộc cung nhỏ BCBC), cắt BCBC tại FF, cắt ACAC tại II. Chứng minh rằng \widehat{MBC}=\widehat{BAC}MBC=BAC . Từ đó suy ra MBICMBIC là tứ giác nội tiếp.
theo gt, ta co:
goc MBC= BAC (cung chan cung BC)
mat khac, ta lai co goc BAC = MIC ( dong vi)
=> goc MBC= MIC
=> tu giac BICM noi tiep