2 câu khoanh tròn thôi ạ
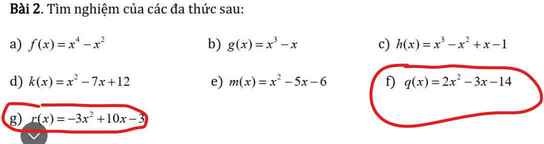
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(c,\) Để PT có 2 nghiệm \(x_1;x_2\Leftrightarrow\Delta=\left(m-4\right)^2+8\left(m-2\right)\ge0\)
\(\Leftrightarrow m^2-8m+16+8m-16\ge0\\ \Leftrightarrow m^2\ge0\left(\text{luôn đúng}\right)\)
Do đó PT có 2 nghiệm với mọi m
\(\text{Viét: }\left\{{}\begin{matrix}x_1+x_2=\dfrac{m-4}{m-2}\left(1\right)\\x_1x_2=\dfrac{2}{2-m}\left(2\right)\end{matrix}\right.\)
Kết hợp \(x_1-x_2=3\text{ với }\left(1\right)\text{ ta được}\)
\(\left\{{}\begin{matrix}x_1=\left(\dfrac{m-4}{m-2}+3\right):2=\dfrac{4m-10}{m-2}\cdot\dfrac{1}{2}=\dfrac{2m-5}{m-2}\\x_2=\dfrac{m-4}{m-2}-\dfrac{2m-5}{m-2}=\dfrac{1-m}{m-2}\end{matrix}\right.\)
Thay vào \(\left(2\right)\Leftrightarrow\dfrac{\left(2m-5\right)\left(1-m\right)}{\left(2-m\right)^2}=\dfrac{2}{2-m}\)
\(\Leftrightarrow\left(2m-5\right)\left(1-m\right)=2\left(2-m\right)\\ \Leftrightarrow7m-2m^2-5=4-2m\\ \Leftrightarrow2m^2-9m+9=0\\ \Leftrightarrow\left[{}\begin{matrix}m=3\\m=\dfrac{3}{2}\end{matrix}\right.\)
Vậy \(m=3\text{ và }m=\dfrac{3}{2}\) thỏa đề bài

`#3107.101107`
Câu 1:
a.
`(1)` Vô cùng nhỏ
`(2)` Trung hòa về điện
`(3)` hạt nhân
`(4)` điện tích dương
`(5)` vỏ nguyên tử
`(6)` các electron
`(7)` điện tích âm
b.
`(8)` chuyển động
`(9)` sắp xếp
c.
`(10)` electron
`(11)` hạt nhân

3 A
4 D
5 A
6 C
7 C
8 A
9 A
10 C
11 C
12 A
13 A
14 B
15 A
16 D
17 D
18 C
19 D
20 D
21 C
22 C
23 C
24 C
25 C
Ex2
1 remember
2 read
3 be repaired
4 focus
5 not enter
6 apoligize
7 attend
8 sit
9 think
10 drive
11 be taken
12 reduce
13 allow
14 regulated
15 swim
16 monitor
17 out
18 be invited
19 send
20 work


13) để căn thức xác định \(\Rightarrow\dfrac{2x-4}{-2}\ge0\) mà \(-2< 0\Rightarrow2x-4\le0\)
\(\Rightarrow x-2\le0\Rightarrow x\le2\)
14) để căn thức xác định \(\Rightarrow-\dfrac{2}{x-2}\ge0\Rightarrow\dfrac{2}{x-2}\le0\)
mà \(2>0\Rightarrow x-2< 0\Rightarrow x< 2\)
15) để căn thức xác định \(\Rightarrow\dfrac{2\sqrt{15}-\sqrt{59}}{7-x}\ge0\)
Ta có: \(2\sqrt{15}=\sqrt{60}>\sqrt{59}\left(60>59\right)\Rightarrow2\sqrt{15}-\sqrt{59}>0\)
\(\Rightarrow7-x>0\Rightarrow x< 7\)
3) để căn thức xác định \(\Rightarrow\left\{{}\begin{matrix}1-x\ge0\\3-x\ge0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x\le1\\x\le3\end{matrix}\right.\Rightarrow x\le1\)
4) để căn thức xác định \(\Rightarrow\left\{{}\begin{matrix}15-3x\ge0\\5-x\ge0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x\le5\\x\le5\end{matrix}\right.\Rightarrow x\le5\)
5) để căn thức xác định \(\Rightarrow\left\{{}\begin{matrix}3x-9\ge0\\9-x\ge0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x\ge3\\x\le9\end{matrix}\right.\Rightarrow3\le x\le9\)
Bài 1:
1) \(\sqrt{2}< \sqrt{3}\)
2) \(\sqrt{3}< \sqrt{10}\)
3) \(2\sqrt{3}>2\sqrt{2}\)
4) \(3\sqrt{3}< 3\sqrt{5}\)
5) \(5\sqrt{2}>3\sqrt{2}\)
6) \(-5\sqrt{3}< -3\sqrt{3}\)
\(f,q\left(x\right)=2x^2-3x-14=0\\ \Leftrightarrow\left(2x^2+4x\right)-\left(7x+14\right)=0\\ \Leftrightarrow2x\left(x+2\right)-7\left(x+2\right)=0\\ \Leftrightarrow\left(x+2\right)\left(2x-7\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=-2\\x=\dfrac{7}{2}\end{matrix}\right.\)
\(g,r\left(x\right)=-3x^2+10x-3=0\\ \Leftrightarrow\left(-3x^2+9x\right)+\left(x-3\right)=0\\ \Leftrightarrow-3x\left(x-3\right)+\left(x-3\right)=0\\ \Leftrightarrow\left(-3x+1\right)\left(x-3\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{3}\\x=3\end{matrix}\right.\)