tìm a và b biết ( 50a + 7b + 3 )( 50 mũ a + 50a + b ) bằng 803
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


- ngocduong516
- 06/12/2021
ta có : 803 là số lẻ
=> ( 50a + 7b + 3 )( 50^a + 50a + b ) là số lẻ
=> 50a + 7b + 3 và 50^a + 50a + b là số lẻ
TH1 : nếu a khác 0
=> 50^a + 50a là là số chẵn
mà 50^a + 50a + b là số lẻ ( theo trên )
=> b lẻ
=> 50b + 3 chẵn
=> 50a + 7b + 3 chẵn ( loại )
TH2 : a = 0
=> (7b+3)(b+1) = 803 = 1. 803 = 11.73
vì b thuộc N
=> 7b + 3 > b+1
do đó
7b + 3 = 803 và b +1 = 1 => loại
hoặc 7b+3 = 73 và b +1 = 11 => b = 50
vậy a = 0 và b = 100

Giải:
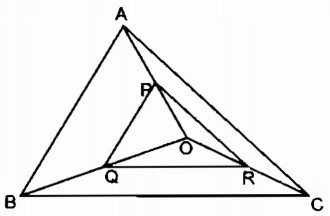
a. Trong tam giác AOB, ta có:
P trung điểm của OA (gt)
Q trung điểm của OB (gt)
Suy ra: PQ là đường trung bình của ∆ OAB.
Suy ra: PQ=12ABPQ=12AB
(tính chất đường trung bình của tam giác )
Suy ra: PQAB=12PQAB=12 (1)
Trong tam giác OAC, ta có:
P trung điểm của OA (gt)
R trung điểm của OC (gt)
Suy ra: PR là đường trung bình của tam giác OAC.
Suy ra: PR=12ACPR=12AC (tính chất đường trung bình của tam giác )
Suy ra: PRAC=12PRAC=12 (2)
Trong tam giác OBC, ta có:
Q trung điểm của OB (gt)
R trung điểm của OC (gt)
Suy ra: QR là đường trung bình của tam giác OBC.
Suy ra: QR=12BCQR=12BC (tính chất đường trung bình của tam giác )
Suy ra: QRBC=12QRBC=12 (3)
Từ (1), (2) và (3) suy ra: PQAB=PRAC=QRBC=12PQAB=PRAC=QRBC=12
Vậy ∆ PQR đồng dạng ∆ ABC (c.c.c)
b. Gọi p’ là chu vi tam giác PQR.
Ta có: PQAB=PRAC=QRBC=PQ+PR+QRAB+AC+BC=p′pPQAB=PRAC=QRBC=PQ+PR+QRAB+AC+BC=p′p
Vậy: p′p=12⇒p′=12p=12.543=271,5p′p=12⇒p′=12p=12.543=271,5 (cm)

a: \(=5\sqrt{2}\cdot a^2\cdot b^3\cdot\sqrt{ab}\)
b: \(=\dfrac{1}{2}\cdot x^2\cdot\left|x-1\right|\)




Làm hộ mình nha