Cho hình thang ABCD có ABDC, AB \(\frac{1}{2}\)DC; AE = \(\frac{1}{3}\)AB. Diện tích hình tam giác EDC là 30cm2 .Tính diện thích hình thang ABCD.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a:Xét ΔBDC vuông tại B và ΔHBC vuông tại H có
góc C chung
=>ΔBDC đồng dạng với ΔHBC
b: \(BD=\sqrt{25^2-15^2}=20\left(cm\right)\)
HC=15^2/25=9cm
HD=25-9=16cm

Độ dài cạnh DM là : 6 nhân 1/3 = 2 (cm)
Diện tích hình thang ABCD là : ( 3 + 6) nhân 3 / 2 = 13,5 (cm2)
Diện tích hình tam giác BMC là : 6 nhân 3 / 2 = 9 ( cm2)
Đ/S : .....

Độ dài DM là : 6 x\(\frac{1}{3}\)= 2 ( cm )
Diện tích hình thang ABCD là : ( 3 + 6 ) x 3 : 2 = 13,5 ( \(cm^2\))
Diện tích tam giác BMC là : 6 x 3 : 2 = 4 (\(cm^2\) )
a) diện tích hình thang ABCD là : 13,5 \(cm^2\)
b) diện tích hình tam giác BMC là : 4\(cm^2\)
cho hình thang ABCD vuông tại A và D . Có AB=AD=\(\frac{DC}{2}\). Tính các góc B và C của hình thang


Đáp án cần chọn là: C
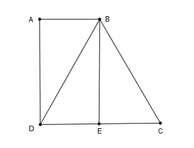
Từ B kẻ BE vuông góc với CD tại E.
Tứ giác ABED là hình thang có hai cạnh bên AD // BE nên AD = BE, AB = DE.
Mặt khác, DC = BC = 2AB nên DC = 2ED, do đó E là trung điểm của DC.
Xét ΔBDE và ΔBCE có B E D ^ = B E C ^ = 90 ° ; DE = EC
BE cạnh chung nên ΔBED = ΔBEC (c – g – c)
Suy ra BD = BC mà BC = DC (gt) => BD = BC = CD nên ΔBCD đều.
Xét ΔBCD đều có BE là đường cao cũng là đường phân giác nên
E B C ^ = 1 2 D B C ^ = 1 2 × 60 ° = 30 °
Vì AD // BE mà B A D ^ = 90 ° nên A B E ^ = 180 ° - B A D ^ = 180 ° - 90 ° = 90 ° (hai góc trong cũng phía bù nhau)
Từ đó A B C ^ = A B E ^ + E B C ^ = 90 ° + 30 ° = 120 °
Vậy A B C ^ = 120 °
Chiều cao của hình thang là :
90 x 2 : 12 = 15 ( cm )
Đáy lớn là :
12 : 3/4 = 16 ( cm )
Diện tích hình thang là ;
( 12 + 16 ) : 2 x 15 = 210 (cm2)
Đáp số: 210 cm2
bạn lấy 90 đau ra v