Một ca nô xuôi một khúc sông hết 3 giờ và ngược khúc sông đó hết 5 giờ. Biết vận tốc
dòng nước là 3km/giờ.
a) Vận tốc khi xuôi dòng lớn hơn vận tốc ngược dòng bao nhiêu km/giờ?
b) Tính vận tốc của ca nô khi xuôi dòng và khi ngược dòng.
c) Tính độ dài khúc sông
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi vận tốc thực của ca nô là V , Vn = 3km/h
t1 = 3 giờ; t2 = 4,5 giờ .
Theo bài ra , ta có : \(AB=\left(V+Vn\right).3=\left(V-Vn\right).4,5\)
\(\Leftrightarrow3V+9=4,5V-13,5\Leftrightarrow3V+9+13,5=4,5V\)
\(\Leftrightarrow1,5V=22,5\Leftrightarrow V=15\left(\frac{km}{h}\right)\Rightarrow\hept{\begin{cases}V+Vn=18\frac{km}{h}\\V-Vn=12\frac{km}{h}\end{cases}}\)
\(\Rightarrow AB=3.\left(V+Vn\right)=3.18=54km.\)
Vậy vận tốc xuôi là 18 km/h , vận tốc ngược dòng là 12 km/h, độ dài khúc sông AB là 54 km.

Gọi vận tốc ca nô khi nước yên lặng là x ( > 3; km/h)
Vận tốc ca nô xuôi dòng là: x + 3 ( km/h)
Vận tốc ca nô khi ngược dòng là: x -3 (km/h)
Vì quãng đường không đổi nên ta có phương trình:
1.( x + 3 ) = 2 ( x - 3 )
<=> x = 9 thỏa mãn
Vậy vận tốc khi nước lặng là 9km/h
Gọi vận tốc thực của ca-nô là v (km/h) (v>3)
Vì ca-nô xuôi dòng hết 1 giờ => Quãng đường ca-nô đi ngược dòng là: 2(v-3)
Vì ca-nô đi ngược dòng hết 2 giờ => Quãng đường ca-nô đu xuôi dòng là: 1(v+3)
Vì quãng đường đi xuôi bằng quãng đường đi ngược nên ta có phương trình
2(v-3)=1(v+3)
<=> 2v-6=v+3
<=> 2v-6-v-3=0
<=> v-9=0
<=> v=9 (tmđk)
Vậy vận tốc ca-nô đi nước đứng yên là 9 km/h

Lời giải:
Tỉ số vận tốc xuôi dòng so với ngược dòng: $\frac{4,5}{3}=\frac{3}{2}$
Hiệu vận tốc xuôi dòng và ngược dòng: $3\times 2=6$ (km/h)
Vận tốc ngược dòng: $6:(3-2)\times 2=12$ (km/h)
Vận tốc xuôi dòng: $12\times 3:2=18$ (km/h)

Gọi độ dài khúc sông là a (km).
Thời gian đi xuôi hết 3 giờ nên vận tốc đi xuôi tính theo a là 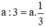 (km/h).
(km/h).
Thời gian đi ngược hết 5 giờ nên vận tốc đi ngược tính theo a là 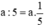 (km/h).
(km/h).
Vận tốc đi xuôi lớn hơn vận tốc đi ngược là: 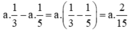 (km/h).
(km/h).
Mà ta có vxuôi = vcano + vnước; vngược = vcano - vnước.
Do đó vxuôi - vngược = 2. vnước = 6km/h.
Vậy 6km/h ứng với 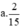 km/h nên suy ra
km/h nên suy ra 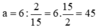
Vậy chiều dài khúc sông là 45km.

Gọi vận tốc dòng ca nô là x (km/h)
Ta có phương trình:
3(x+3) = 5(x-3)
<=> 2x = 24
=> x = 12 (km/h)
=> S = (12+3).3 = 45 (km)
Vậy dòng sông dài 45km

Gọi \(a,b\) lần lượt là vận tốc riêng của ca nô và vận tốc dòng nước \(\left(a>b>0\right)\).
Thời gian ca nô đi xuôi dòng khúc sông \(60km\) là : \(\dfrac{60}{a+b}\left(h\right)\).
Thời gian ca nô đi ngược dòng \(48km\) là : \(\dfrac{48}{a-b}\left(h\right)\).
Theo đề bài thì \(\dfrac{60}{a+b}+\dfrac{48}{a-b}=6\left(1\right)\).
Thời gian ca nô đi xuôi dòng \(40km\) là : \(\dfrac{40}{a+b}\left(h\right)\).
Thời gian ca nô đi ngược dòng \(80km\) là : \(\dfrac{80}{a-b}\left(h\right)\)
Cũng theo đề bài, ta có : \(\dfrac{40}{a+b}+\dfrac{80}{a-b}=7\left(2\right)\).
Từ \((1)\) và \((2)\), ta có hệ phương trình :
\(\left\{{}\begin{matrix}\dfrac{60}{a+b}+\dfrac{48}{a-b}=6\\\dfrac{40}{a+b}+\dfrac{80}{a-b}=7\end{matrix}\right.\left(I\right)\)
Đặt : \(x=\dfrac{20}{a+b}\) và \(y=\dfrac{16}{a-b}\). Hệ \((I)\) được viết lại thành :
\(\left\{{}\begin{matrix}3x+3y=6\\2x+5y=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x+y=2\\2x+5y=7\end{matrix}\right.\)
Hay : \(\left\{{}\begin{matrix}5x+5y=10\\2x+5y=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x=3\\x+y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=1\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{20}{a+b}=1\\\dfrac{16}{a-b}=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a+b=20\\a-b=16\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2a=36\\a+b=20\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=18\\b=2\end{matrix}\right.\) (thỏa mãn).
Vậy : Vận tốc riêng của ca nô là \(18(km/h)\) và vận tốc dòng nước là \(2(km/h).\)
Gọi vận tốc riêng của cano là x (km/h) với x>0
Gọi vận tốc của dòng nước là y (km/h) với y>0 và y<x
Vận tốc cano khi xuôi dòng: \(x+y\) (km/h)
Vận tốc cano khi ngược dòng: \(x-y\) (km/h)
Do cano xuôi dòng 60km và ngược dòng 48km hết 6h nên ta có:
\(\dfrac{60}{x+y}+\dfrac{48}{x-y}=6\)
Do cano xuôi dòng 40km và ngược dòng 80km thì hết 7h nên ta có:
\(\dfrac{40}{x+y}+\dfrac{80}{x-y}=7\)
Ta được hệ: \(\left\{{}\begin{matrix}\dfrac{60}{x+y}+\dfrac{48}{x-y}=6\\\dfrac{40}{x+y}+\dfrac{80}{x-y}=7\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{120}{x+y}+\dfrac{96}{x-y}=12\\\dfrac{120}{x+y}+\dfrac{240}{x-y}=21\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{120}{x+y}+\dfrac{96}{x-y}=12\\\dfrac{144}{x-y}=9\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x-y=16\\\dfrac{120}{x+y}+\dfrac{96}{16}=12\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x-y=16\\x+y=20\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=18\\y=2\end{matrix}\right.\)

Gọi độ dài khúc sông là x.
Ta có vận tốc ca nô khi xuôi dòng là x/3 và vận tốc ca nô lúc ngược dòng là x/5
Vận tốc ca nô xuôi dòng hơn vận tốc ca nô ngược dòng 2 lần vận tốc dong nước nên:
x/3-x/5=6
x=45
Vậy khúc sông dài 45 km.

Độ dài khúc sông bằng quãng đường đi xuôi dòng trong 3 giờ.
Vận tốc xuôi dòng bằng vận tốc thực của ca nô cộng với 3 km/h.
Vận tốc khi ngược dòng bằng vận tốc thực của ca nô trừ đi 3 km/h.
Do đó vận tốc xuôi dòng hơn vận tốc ngược dòng của ca nô là 6 km/h.
Vì trong mỗi giờ quãng đường đi được khi ngược dòng ngắn hơn quãng đường xuôi dòng là 6 km nên trong 3 giờ ngược dòng thì ca nô đi được quãng đường ngắn hơn quãng đường xuôi dòng là
6 . 3 = 18 km;
Tức là ngắn hơn độ dài khúc sông là 18 km.
Để đi hết 18 km này ca nô đã phải ngược dòng thêm 2 giờ nữa.
Do đó vận tốc ngược dòng là: 18 : 2 = 9 (km/h).
Vậy độ dài khúc sông là: 9 . 5 = 45 (km).
Lưu ý: Có thể đưa bài toán trên về bài toán tìm x như sau:
Gọi độ dài khúc sông là x (km).
Vận tốc xuôi dòng của ca nô là: \(\dfrac{x}{3}\) (km/h)
Vận tốc ngược dòng của ca nô là: \(\dfrac{x}{5}\) (km/h).
Vận tốc thực của ca nô bằng: \(\dfrac{x}{3}-3=\dfrac{x}{5}+3\) hay 5x - 45 = 3x + 45
Chuyển vế ta được: 2x = 90. Vậy x = 45 (km).
Gọi x(km/h)là vận tốc của ca nô
Khi ca nô xuôi dòng thì mất 3h nên độ dài của khúc sông là 3(x+3)km
Khi ca nô đi ngược về thì mất 5h nên độ dài của khúc sông là 5(x-3)km
Vì 5(x-3)=3(x+3)
=>5x-15=3x+9
=>2x=24
Vậy x=12
Khúc sông là 3(12+3)=45

Gọi chiều dài khúc sông là s ( km ).
Vận tốc thực của ca nô là v ( km/h )
=> vận tốc xuôi dòng là v+3 , ngược dòng là v -3
Do canô xuôi dòng hết 3h
=> s = 3(v+3) (1)
Do canô ngược dòng đó hết 5h
=> s = 5(v-3) (2)
Từ (1) và (2) => 3(v+3) = 5(v-3)
=> 3v+9 = 5v - 15
=> 2v = 24
=> v = 12
Thay v =12 vào (1) ta có s = 3(12+3) = 45
Vậy khúc sông dài 45 km
tổng số giờ ca nô đi xuôi và đi ngược là :
3 +5 = 8 ( giờ )
độ dài khúc sông là :
8x3= 24 ( km )
đúng 100%
mk nha
Vận tốc khi xuôi dòng lớn hơn vận tốc ngược dòng là:
\(3\times2=6\left(km/h\right)\)
Mỗi giờ đi xuôi dòng được số phần khúc sông là:
\(1\div3=\frac{1}{3}\)(khúc sông)
Mỗi giờ đi ngược dòng được số phần khúc sông là:
\(1\div5=\frac{1}{5}\)(khúc sông)
Mỗi giờ xuôi dòng đi được nhiều hơn mỗi phần ngược dòng là:
\(\frac{1}{3}-\frac{1}{5}=\frac{2}{15}\)(khúc sông)
Mỗi giờ dòng nước chảy số phần khúc sông là:
\(\left(\frac{1}{3}-\frac{1}{5}\right)\div2=\frac{1}{15}\)(khúc sông)
Độ dài khúc sông là:
\(3\div\frac{1}{15}=45\left(km\right)\)
Vận tốc xuôi dòng là:
\(45\div3=15\left(km\right)\)
Vận tốc ngược dòng là:
\(45\div5=9\left(km\right)\)