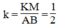Cho HCN MNDQ,vẽ NK vuông góc với MD
a)CMR:Tam giác KMN đồng dạng với Tam giác QPM và MN2=KM.PM
b)Gọi I là trung điểm của MK,E là trung điểm của KN
CMR:Tam giác IKE đồng dạng với Tam giác PQM và IK.PM=IE.PM
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
27 tháng 5 2021
Bài 1:
a) Xét tam giác ABE và tam giác ACF có:
Góc AEB=góc AFC(=90 độ)
Góc A chung
=>Tam giác ABE đồng dạng vs tam giác ACF (g-g)
b)
Vì tam giác ABE đồng dạng vs tam giác ACF(cmt)
=>\(\frac{AB}{AC}=\frac{AE}{AF}\)
Xét tam giác AFE và tam giác ACB có:
Góc A chung(gt)
\(\frac{AB}{AC}=\frac{AE}{AF}\)
=>Tam giác AFE và tam giác ACB đồng dạng (c-g-c)
c)
H ở đou ra vại? :))
27 tháng 2 2021
tự kẻ hình ná
trong tam giác AHC có
AK=KH
HN=CN
=> KN là đtb=> KN//AC và KN=AC/2
tương tự, ta có MK//AB và MK=AB/2
MN//BC và MN=BC/2
Xét tam giác ABC và tam giác KMN có
KN/AC=MN/BC=MK/AB(=1/2) (cũng là tỉ số đồng dạng của 2 tam giác)
=> tam giác ABC đồng dạng với tam giác KMN(ccc)
CM
3 tháng 5 2017
* Trong △ AHB, ta có:
K trung điểm của AH (gt)
M trung điểm của BH (gt)
Suy ra KM là đường trung bình của tam giác AHB.
Suy ra: KM = 1/2 AB (tính chất đường trung bình của tam giác)
Suy ra: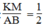 
(1)
* Trong △ AHC, ta có:
K trung điểm của AH (gt)
N trung điếm của CH (gt)
Suy ra KN là đường trung bình của tam giác AHC.
Suy ra: KN =1/2 AC (tính chất đường trung bình của tam giác)
Suy ra: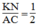 
(2)
* Trong △ BHC, ta có:
M trung điểm của BH (gt)
N trung điểm của CH (gt)
Suy ra MN là đường trung bình của tam giác BHC.
Suy ra: MN = 1/2 BC (tính chất đường trung bình của tam giác)
Suy ra: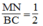 
(3)
Từ (1), (2) và (3) suy ra: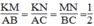 
Vậy △ KMN đồng dạng △ ABC (c.c.c)
Ta có: 