HELP mình với
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HH
7
HT
12
4 tháng 1 2023
a, (1) \(2Al+6HCl\rightarrow2AlCl_3+3H_2\)
(2) \(AlCl_3+3NaOH\rightarrow3NaCl+Al\left(OH\right)_{3\downarrow}\)
\(2Al\left(OH\right)_3\underrightarrow{t^o}Al_2O_3+3H_2O\)
(4) \(2Al_2O_3\underrightarrow{đpnc}4Al+3O_2\)
b, (1) \(2Fe+3Cl_2\underrightarrow{t^o}2FeCl_3\)
(2) \(FeCl_3+3NaOH\rightarrow3NaCl+Fe\left(OH\right)_{3\downarrow}\)
(3) \(2Fe\left(OH\right)_3\underrightarrow{t^o}Fe_2O_3+H_2O\)
(4) \(Fe_2O_3+3H_2\underrightarrow{t^o}2Fe+3H_2O\)
(5) \(Fe+2HCl\rightarrow FeCl_2+H_2\)
c, (1) \(2Al_2O_3\underrightarrow{đpnc}4Al+3O_2\)
(2) \(2Al+3H_2SO_4\rightarrow Al_2\left(SO_4\right)_3+3H_2\)
(3) \(Al_2\left(SO_4\right)_3+3BaCl_2\rightarrow3BaSO_{4\downarrow}+2AlCl_3\)
(4) \(AlCl_3+3NaOH\rightarrow3NaCl+Al\left(OH\right)_{3\downarrow}\)
d, (1) \(S+O_2\underrightarrow{t^o}SO_2\)
(2) \(2SO_2+O_2\xrightarrow[V_2O_5]{t^o}2SO_3\)
(3) \(SO_3+H_2O\rightarrow H_2SO_4\)
(4) \(H_2SO_4+2NaOH\rightarrow Na_2SO_4+2H_2O\)
(5) \(Na_2SO_4+BaCl_2\rightarrow2NaCl+BaSO_{4\downarrow}\)
e, (1) \(2Al_2O_3\underrightarrow{đpnc}4Al+3O_2\)
(2) \(2Al+6HCl\rightarrow2AlCl_3+3H_2\)
(3) \(AlCl_3+3NaOH\rightarrow3NaCl+Al\left(OH\right)_{3\downarrow}\)
(4)
(5) \(NaAlO_2+CO_2+2H_2O\rightarrow Al\left(OH\right)_{3\downarrow}+NaHCO_3\)
HT
5
IO
13 tháng 12 2021
3x . 2 + 15 = 33
3x . 2 = 33 - 15 = 18
3x = 18 : 2 = 9 = 32
=> x = 2
Y
11 tháng 7 2023
\(1,x=16\Rightarrow A=\dfrac{16-1}{\sqrt{16}}=\dfrac{15}{4}\)
\(2,B=\dfrac{\sqrt{x}+1}{\sqrt{x}-1}-\dfrac{\sqrt{x}-1}{\sqrt{x}+1}+4\sqrt{x}\left(dl:x>0,x\ne1\right)\)
\(=\dfrac{\left(\sqrt{x}+1\right)^2-\left(\sqrt{x}-1\right)^2+4\sqrt{x}\left(x-1\right)}{x-1}\\ =\dfrac{x+2\sqrt{x}+1-x+2\sqrt{x}-1+4x\sqrt{x}-4\sqrt{x}}{x-1}\\ =\dfrac{4x\sqrt{x}}{x-1}\)
\(3,P=A.B=\dfrac{x-1}{\sqrt{x}}.\dfrac{4x\sqrt{x}}{x-1}=4x\)
\(\sqrt{P}>P\Leftrightarrow\sqrt{4x}>4x\Leftrightarrow\left(\sqrt{4x}\right)^2>\left(4x\right)^2\Leftrightarrow4x>16x^2\Leftrightarrow4x-16x^2>0\Leftrightarrow4x\left(1-4x\right)>0\)
\(\Leftrightarrow\left[{}\begin{matrix}4x>0\\1-4x>0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x>0\\x< \dfrac{1}{4}\end{matrix}\right.\)
Vậy \(S=\left\{x|0< x< \dfrac{1}{4}\right\}\) thì \(\sqrt{P}>P\)
\(4,\left|P\right|>P\Leftrightarrow\left|4x\right|>4x\)
\(TH_1:x\ge0\\4x>4x\Leftrightarrow4x-4x>0\Leftrightarrow0>0\left(VL\right) \)
\(TH_2:x< 0\\ -4x>4x\Leftrightarrow-4x-4x>0\Leftrightarrow-8x>0\Leftrightarrow x< 0\)
Vậy \(x< 0\) thì \(\left|P\right|>P\)
XB
10 tháng 1 2023
Gọi \(x\) là số học sinh giỏi lớp 5A. Theo đề bài ta có:
\(x\) x \(\dfrac{3}{5}\) = 6 ⇒ \(x\) = 6 x \(\dfrac{5}{3}\) = 10 (học sinh)
Vậy lớp 5A có 10 học sinh giỏi
9 tháng 1 2023
Số học sinh lớp 5A là:
6 : \(\dfrac{3}{5}\)
= 10 ( em)
Đ/S: 10 em
19 tháng 12 2021
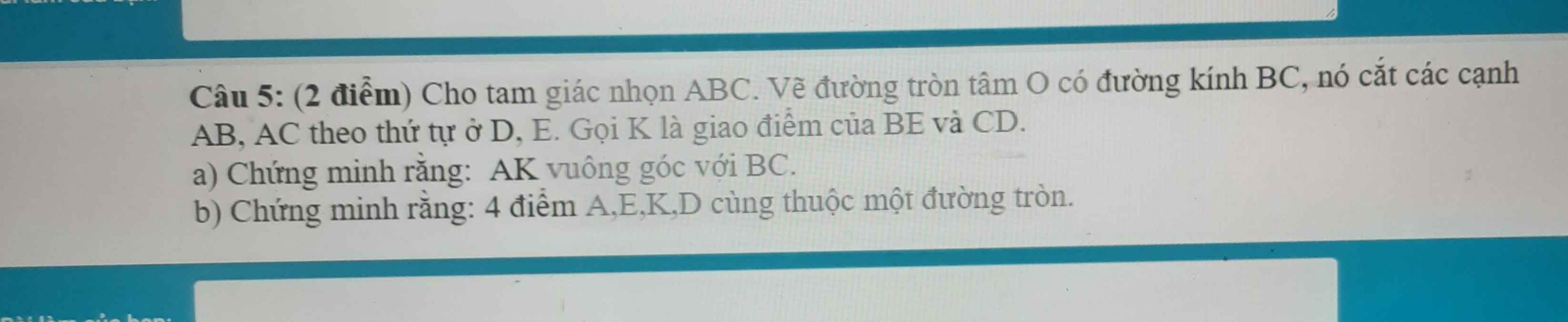
a: Xét (O) có
ΔBDC nội tiếp
BC là đường kính
Do đó: ΔBDC vuông tại D
Xét (O) có
ΔBEC nội tiếp
BC là đường kính
Do đó: ΔEBC vuông tại E
Xét ΔABC có
BE là đường cao
CD là đường cao
BE cắt CD tại K
Do đó: AK⊥BC
27 tháng 12 2021
a: Xét ΔABE và ΔACE có
AB=AC
AE chung
BE=CE
Do đó: ΔABE=ΔACE
help mình với :(
5 tháng 1 2022
a: a⊥AB
b⊥AB
Do đó: a//b
b: \(\widehat{D_1}+\widehat{C_1}=180^0\)
nên \(\widehat{C_1}=60^0\)
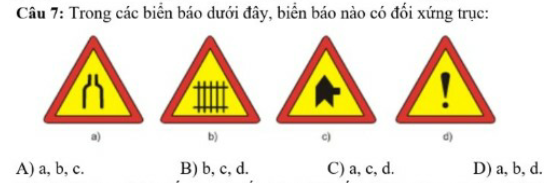
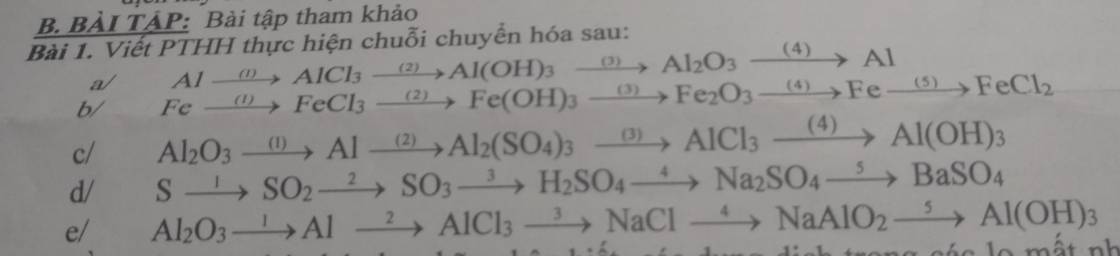
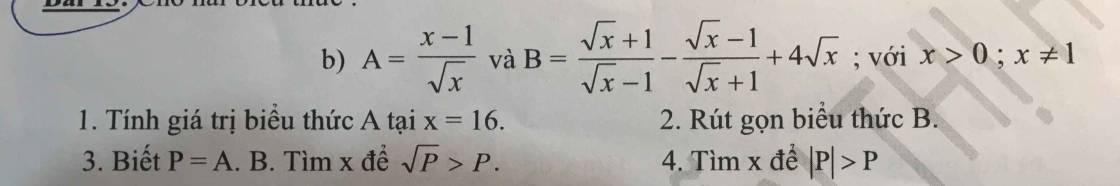
b3 cuối em cm hệt như này:
Bài 3:
a: Thay m=-1/2 vào (1),ta được:
\(x^2-2\cdot\left(2-\dfrac{1}{2}\right)x+2\cdot\dfrac{-1}{2}+1=0\)
\(\Leftrightarrow x^2-3x=0\)
=>x=0 hoặc x=3
b: \(\Delta=\left(2m+4\right)^2-4\left(2m+1\right)\)
\(=4m^2+16m+16-8m-4\)
\(=4m^2+8m+12\)
\(=4m^2+8m+4+8=\left(2m+2\right)^2+8>0\)
Do đó: Phương trình luôn có hai nghiệm phân biệt
Theo đề, ta có: \(\left(x_1+x_2\right)^2-2x_1x_2=6\)
\(\Leftrightarrow\left(2m+4\right)^2-2\left(2m+1\right)=6\)
\(\Leftrightarrow4m^2+16m+16-4m-2-6=0\)
\(\Leftrightarrow4m^2+12m+8=0\)
\(\Leftrightarrow\left(m+1\right)\left(m+2\right)=0\)
=>m=-1 hoặc m=-2