Giúp em hai bài này với ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
20 tháng 8 2021
Bạn làm thiếu rồi nhé. Đoạn này lúc đầu mình cũng phân vân nhưng vẫn tính được x và y
HP
20 tháng 8 2021
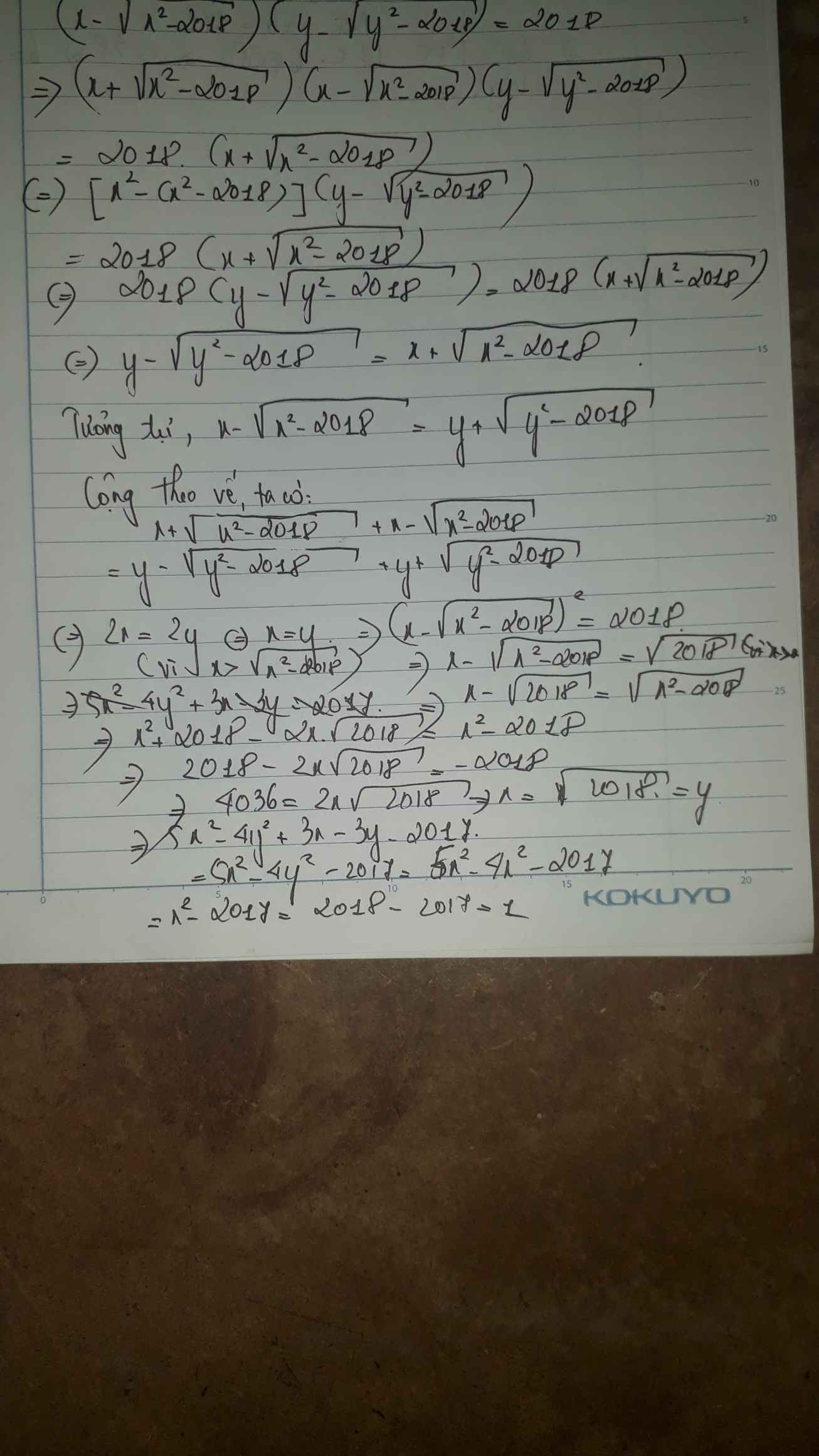
1.
ĐK: \(x,y\ge\sqrt{2018};x,y\le-\sqrt{2018}\)
\(\left(x-\sqrt{x^2-2018}\right)\left(y^2-2018\right)=2018\left(1\right)\)
\(\Leftrightarrow\left(x-\sqrt{x^2-2018}\right)\left(y-\sqrt{y^2-2018}\right)=2018\)
\(\Leftrightarrow2018\left(y-\sqrt{y^2-2018}\right)=2018\left(x+\sqrt{x^2-2018}\right)\)
\(\Leftrightarrow y-\sqrt{y^2-2018}=x+\sqrt{x^2-2018}\left(2\right)\)
Mặt khác:
\(\left(1\right)\Leftrightarrow2018\left(x-\sqrt{x^2-2018}\right)=2018\left(y+\sqrt{y^2-2018}\right)\)
\(\Leftrightarrow x-\sqrt{x^2-2018}=y+\sqrt{y^2-2018}\left(3\right)\)
Trừ vế theo vế (2) cho (3):
\(y-\sqrt{y^2-2018}-x+\sqrt{x^2-2018}=x+\sqrt{x^2-2018}-y-\sqrt{x^2-2018}\)
\(\Leftrightarrow x=y\)
Khi đó:
\(5x^2-4y^2+3x-3y-2017=x^2-2017\)
D
1
10 tháng 10 2023
Bài 1.
a,Vì \(\dfrac{a}{b}>1\)=>a<b
Với m∈N* Ta có
\(am> bm\)=>\(am+ab> bm+ab\)=>\(a\left(b+m\right)> b\left(a+m\right)\)=>\(\dfrac{a}{b}>\dfrac{a+m}{b+m} \)
b, Vì \(\dfrac{a}{b}< 1\)=>a<b
Với m∈N* =>
\(am< bm\)=>\(am+ab< bm+ab\)=>\(a\left(b+m\right)< b\left(a+m\right)\)=>\(\dfrac{a}{b}<\dfrac{a+m}{b+m} \)
Tự áp dụng cho bài 2 nhé bạn :)
3T
0
HA
0
DT
0
Q
28 tháng 7 2021
lần đổ 1
\(\left(mC+m'C'\right).\left(38-20\right)=mC.\left(60-38\right)\)
\(\Leftrightarrow\left(mC+m'C'\right)18=mC.22\)
\(\Leftrightarrow2mC=9m'C'\)
lần 2 \(\left(2mC+m'C'\right)\left(t_x-38\right)=mC.\left(60-t_x\right)\)
\(11m'C'\left(t_x-38\right)=\dfrac{9}{2}.m'C'\left(60-t_x\right)\)
\(\Rightarrow t_x=...\)
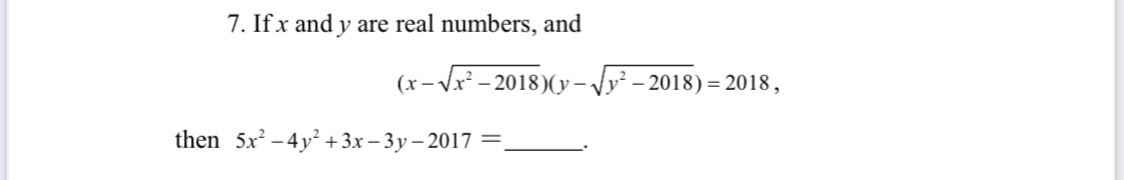
giúp em 3 bài này với ạ em đang cần gấp chiều em hc ròi ạ ai làm đc bài nào thì gửi luôn giúp em ạ
a: 3-5/7=21/7-5/7=16/7
b: 21/9-2=21/9-18/9=3/9=1/3
c: 15/4-2/3-3/4=12/4-2/3=3-2/3=7/3
a,\(\dfrac{16}{7}\)
b, \(\dfrac{1}{3}\)
c,\(\dfrac{7}{3}\)