cho tam giác ABC có AB =5 BC= 7 CA = 8. số đo góc A bằng ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Theo hệ quả định lí cosin, ta có cos A ^ = A B 2 + A C 2 − B C 2 2 A B . A C = 5 2 + 8 2 − 7 2 2.5.8 = 1 2 .
Do đó, A ^ = 60 ° .
Chọn C.

a.
\(BC=\sqrt{AB^2+AC^2-2AB.AC.cosA}=7\)
\(S=\dfrac{1}{2}AB.AC.sinA=10\sqrt{3}\)
\(\Rightarrow h_a=\dfrac{2S}{BC}=\dfrac{20\sqrt{3}}{7}\)
\(R=\dfrac{BC}{2sinA}=\dfrac{7\sqrt{3}}{3}\)
b.
\(cosA=\dfrac{AB^2+AC^2-BC^2}{2AB.AC}=-\dfrac{11}{34}\)
\(\Rightarrow sinA=\dfrac{3\sqrt{115}}{34}\)
\(S=\dfrac{1}{2}AB.AC.sinA=6\sqrt{115}\)
\(h_a=\dfrac{2S}{BC}=\dfrac{4\sqrt{115}}{7}\)
\(R=\dfrac{BC}{2sinA}=...\)

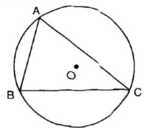
Các cung 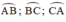 tạo thành một đường tròn
tạo thành một đường tròn
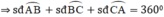
⇒ x + 75 ° + 2 x + 25 ° + 3 x − 22 ° = 360 ° ⇒ 6 x = 282 ° ⇒ x = 47 °
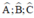 là các góc nội tiếp chắn các cung
là các góc nội tiếp chắn các cung 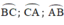
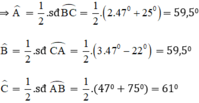
Vậy chọn đáp án C.

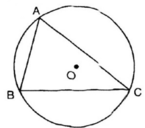
Các cung 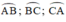 tạo thành một đường tròn
tạo thành một đường tròn
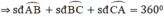
⇒ x + 75 ° + 2 x + 25 ° + 3 x − 22 ° = 360 ° ⇒ 6 x = 282 ° ⇒ x = 47 °
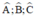 là các góc nội tiếp chắn các cung
là các góc nội tiếp chắn các cung 
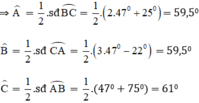
Vậy chọn đáp án C.

Bài 5:
Tgiac ABC vuông cân tại A => góc CBA = 45 độ
Xét góc CBA là góc ngoài tgiac DBC => góc CBA = góc D + DCB
Xét tgiac DBC có DB = BC => tgiac DBC cân tại B => góc D = góc DBC
=> góc D = 45/2 = 22,5 độ
và góc ACD = 22,5 + 45 = 67,5 độ
Vậy số đo các góc của tgiac ACD là ...
Bài 6:
Tgiac ABC cân tại B, góc B = 100 độ => góc A = góc C = 40 độ
Xét tgiac ABD có AB = AD => tgiac ABD cân tại A => góc EDB (ADB) = (180-40)/2 =70 độ
cmtt với tgiac CBE => góc DEB = 70 độ
=> góc DBE = 180-70-70 = 40 độ
Bài 7:
Xét tgiac ABC cân tại A => góc BAC = 180 - 2.góc C => 2.(90 - góc C)
Xét tgiac BHC vuông tại H => góc CBH = 90 - góc C
=> đpcm
Bài 8: mai làm hihi

Có
\(AB^2=10^2\)
\(BC^2+AC^2=36+64=10^2\)
=> \(AB^2=AC^2+BC^2\)
=> t/g ABC vuông tại C
=> \(\widehat{ACB}=90^o\)

b: Độ dài cạnh huyền là \(\sqrt{6^2+7^2}=\sqrt{85}\left(cm\right)\)
c: Số đo góc ở đỉnh là:
\(180-2\cdot20^0=140^0\)
d: Số đó góc ở đáy là:
\(\dfrac{180^0-60^0}{2}=60^0\)

Lời giải:
Ta có : \(\Delta ABC\)là tam giác đều => \(\widehat{A}=\widehat{B}=\widehat{C}\)
Xét tam giác AFD và tam giác BED có :
AD = BE (gt)
\(\widehat{FAD}=\widehat{EBD}=60^0\)
AF = BD (gt)
=> \(\Delta AFD=\Delta BED\left(c-g-c\right)\)
=> DE = DF (hai cạnh tương ứng) (1)
Xét tam giác ADF và tam giác CEF có :
AD = CE (gt)
\(\widehat{DAF}=\widehat{ECF}=60^0\)
AF = CF (gt)
=> \(\Delta ADF=\Delta CEF\)(c-g-c)
=> DF = EF (hai cạnh tương ứng) (2)
Từ (1) và (2) => DE = DF = EF
Vậy \(\Delta DEF\)là tam giác đều
\(cosA=\dfrac{AB^2+AC^2-BC^2}{2AB.AC}=\dfrac{5^2+8^2-7^2}{2.5.8}=\dfrac{1}{2}\)
\(\Rightarrow A=60^0\)