tìm x để đạt giá trị nguyên
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1:
a) Ta có: \(P=1+\dfrac{3}{x^2+5x+6}:\left(\dfrac{8x^2}{4x^3-8x^2}-\dfrac{3x}{3x^2-12}-\dfrac{1}{x+2}\right)\)
\(=1+\dfrac{3}{\left(x+2\right)\left(x+3\right)}:\left(\dfrac{8x^2}{4x^2\left(x-2\right)}-\dfrac{3x}{3\left(x-2\right)\left(x+2\right)}-\dfrac{1}{x+2}\right)\)
\(=1+\dfrac{3}{\left(x+2\right)\left(x+3\right)}:\left(\dfrac{4}{x-2}-\dfrac{x}{\left(x-2\right)\left(x+2\right)}-\dfrac{1}{x+2}\right)\)
\(=1+\dfrac{3}{\left(x+2\right)\left(x+3\right)}:\dfrac{4\left(x+2\right)-x-\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}\)
\(=1+\dfrac{3}{\left(x+2\right)\left(x+3\right)}\cdot\dfrac{\left(x-2\right)\left(x+2\right)}{4x+8-x-x+2}\)
\(=1+3\cdot\dfrac{\left(x-2\right)}{\left(x+3\right)\left(2x+10\right)}\)
\(=1+\dfrac{3\left(x-2\right)}{\left(x+3\right)\left(2x+10\right)}\)
\(=\dfrac{\left(x+3\right)\left(2x+10\right)+3\left(x-2\right)}{\left(x+3\right)\left(2x+10\right)}\)
\(=\dfrac{2x^2+10x+6x+30+3x-6}{\left(x+3\right)\left(2x+10\right)}\)
\(=\dfrac{2x^2+19x-6}{\left(x+3\right)\left(2x+10\right)}\)

\(1,\\ a,=6x^4-15x^3-12x^2\\ b,=x^2+2x+1+x^2+x-3-4x=2x^2-x-2\\ c,=2x^2-3xy+4y^2\\ 2,\\ a,=7x\left(x+2y\right)\\ b,=3\left(x+4\right)-x\left(x+4\right)=\left(3-x\right)\left(x+4\right)\\ c,=\left(x-y\right)^2-z^2=\left(x-y-z\right)\left(x-y+z\right)\\ d,=x^2-5x+3x-15=\left(x-5\right)\left(x+3\right)\\ 3,\\ a,\Leftrightarrow3x\left(x+2\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-2\end{matrix}\right.\\ b,\Leftrightarrow\left(x-1\right)\left(x+2\right)=0\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-2\end{matrix}\right.\)
Câu 1
a)\(3x^2\left(2x^2-5x-4\right)=6x^4-15x^3-12x^2\)
b)\(\left(x+1\right)^2+\left(x-2\right)\left(x+3\right)-4x=x^2+2x+1+x^2+3x-2x-6-4x=2x^2-x-5\)

c) Để A nhận giá trị nguyên khi và chỉ khi:
![]()
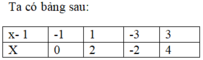
Kết hợp với điều kiện, tập hợp các giá trị của x nguyên để A nguyên là: {0; 2; -2; 4}.

Ta có: \(M=\dfrac{x^5+3x^3-x^2+3x-7}{x^2+2}\)
\(=\dfrac{x^5+2x^3+x^3+2x-x^2-2+x-5}{x^2+2}\)
\(=\dfrac{x^3\left(x^2+2\right)+x\left(x^2+2\right)-\left(x^2+2\right)+\left(x-5\right)}{x^2+2}\)
\(=\dfrac{\left(x^2+2\right)\left(x^3+x-1\right)+\left(x-5\right)}{\left(x^2+2\right)}\)
\(=x^3+x-1+\dfrac{x-5}{x^2+2}\)
Để M nguyên thì \(x-5⋮x^2+2\)
\(\Leftrightarrow\left(x-5\right)\left(x+5\right)⋮x^2+2\)
\(\Leftrightarrow x^2-25⋮x^2+2\)
\(\Leftrightarrow x^2+2-27⋮x^2+2\)
mà \(x^2+2⋮x^2+2\)
nên \(-27⋮x^2+2\)
\(\Leftrightarrow x^2+2\inƯ\left(-27\right)\)
\(\Leftrightarrow x^2+2\in\left\{1;-1;3;-3;9;-9;27;-27\right\}\)
\(\Leftrightarrow x^2+2\in\left\{3;9;27\right\}\)(Vì \(x^2+2\ge2\forall x\))
\(\Leftrightarrow x^2\in\left\{1;7;25\right\}\)
hay \(x\in\left\{1;-1;\sqrt{7};-\sqrt{7};5;-5\right\}\)
Vậy: Để M nguyên thì \(x\in\left\{1;-1;\sqrt{7};-\sqrt{7};5;-5\right\}\)

`@` `\text {Ans}`
`\downarrow`
`1.`
\(\left(-4xy\right)\cdot\left(2xy^2-3x^2y\right)\)
`=`\(\left(-4xy\right)\left(2xy^2\right)+\left(-4xy\right)\left(-3x^2y\right)\)
`=`\(-8\left(x\cdot x\right)\left(y\cdot y^2\right)+12\left(x\cdot x^2\right)\left(y\cdot y\right)\)
`=`\(-8x^2y^3+12x^3y^2\)
`2.`
\(\left(-5x\right)\left(3x^3+7x^2-x\right)\)
`=`\(\left(-5x\right)\left(3x^3\right)+\left(-5x\right)\left(7x^2\right)+\left(-5x\right)\left(-x\right)\)
`=`\(-15x^4-35x^3+5x^2\)
`3.`
\(\left(3x-2\right)\left(4x+5\right)-6x\left(2x-1\right)\)
`=`\(3x\left(4x+5\right)-2\left(4x+5\right)-12x^2+6x\)
`=`\(12x^2+15x-8x-10-12x^2+6x\)
`=`\(\left(12x^2-12x^2\right)+\left(15x-8x+6x\right)-10\)
`=`\(13x-10\)
`4.`
\(2x^2\left(x^2-7x+9\right)\)
`=`\(2x^2\cdot x^2+2x^2\cdot\left(-7x\right)+2x^2\cdot9\)
`=`\(2x^4-14x^3+18x^2\)
`5.`
\(\left(3x-5\right)\left(x^2-5x+7\right)\)
`=`\(3x\left(x^2-5x+7\right)-5\left(x^2-5x+7\right)\)
`=`\(3x^3-15x^2+21x-5x^2+25x-35\)
`=`\(3x^3-20x^2+46x-35\)

\(a,A=\left(x^2-4xy+4y^2\right)+10\left(x-2y\right)+25+\left(y^2-2y+1\right)+2\\ A=\left(x-2y\right)^2+10\left(x-2y\right)+5+\left(y-1\right)^2+2\\ A=\left(x-2y+5\right)^2+\left(y-1\right)^2+2\ge2\)
Dấu \("="\Leftrightarrow\left\{{}\begin{matrix}x=2y-5\\y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-3\\y=1\end{matrix}\right.\)
\(b,\Leftrightarrow3x^3+10x^2-5+n=\left(3x+1\right)\cdot a\left(x\right)\)
Thay \(x=-\dfrac{1}{3}\Leftrightarrow3\left(-\dfrac{1}{27}\right)+10\cdot\dfrac{1}{9}-5+n=0\)
\(\Leftrightarrow-\dfrac{1}{9}+\dfrac{10}{9}-5+n=0\\ \Leftrightarrow-4+n=0\Leftrightarrow n=4\)
\(c,\Leftrightarrow2n^2-4n+5n-10+3⋮n-2\\ \Leftrightarrow2n\left(n-2\right)+5\left(n-2\right)+3⋮n-2\\ \Leftrightarrow n-2\inƯ\left(3\right)=\left\{-3;-1;1;3\right\}\\ \Leftrightarrow n\in\left\{-1;1;3;5\right\}\)

a) y′ = 3 x 2 + 2(m + 3)x + m
y′ = 0 ⇔ 3 x 2 + 2(m + 3)x + m = 0
Hàm số đạt cực trị tại x = 1 thì:
y′(1) = 3 + 2(m + 3) + m = 3m + 9 = 0 ⇔ m = −3
Khi đó,
y′ = 3 x 2 – 3;
y′′ = 6x;
y′′(1) = 6 > 0;
Suy ra hàm số đạt cực tiểu tại x = 1 khi m = 3.
b) y′ = −( m 2 + 6m) x 2 − 4mx + 3
y′(−1) = − m 2 − 6m + 4m + 3 = (− m 2 − 2m – 1) + 4 = −(m + 1)2 + 4
Hàm số đạt cực trị tại x = -1 thì :
y′(−1) = − ( m + 1 ) 2 + 4 = 0 ⇔ ( m + 1 ) 2 = 4
⇔ 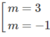
Với m = -3 ta có y’ = 9 x 2 + 12x + 3
⇒ y′′ = 18x + 12
⇒ y′′(−1) = −18 + 12 = −6 < 0
Suy ra hàm số đạt cực đại tại x = -1.
Với m = 1 ta có:
y′ = −7 x 2 − 4x + 3
⇒ y′′ = −14x − 4
⇒ y′′(−1) = 10 > 0
Suy ra hàm số đạt cực tiểu tại x = -1
Kết luận: Hàm số đã cho đạt cực đại tại x = -1 khi m = -3.


