Tính cos(15 mà không sử dụng bảng lượng giác và máy tính bỏ túi.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Với 0 ° < α < 90 ° ta có α tăng thì cos α giảm
Ta có: 40 ° < 75 ° , suy ra cos 40 ° > cos 75 °

Với 0 ° < α < 90 ° ta có α tăng thì sin α tăng
Ta có: 38 ° + 52 ° = 90 ° , suy ra: cos 38 ° = sin 52 °
Vì 38 ° < 52 ° nên sin 38 ° < sin 52 ° hay sin 38 ° < cos 38 °

Với 0 ° < α < 90 ° ta có α tăng thì cos α giảm
Ta có: 40 ° + 50 ° = 90 ° , suy ra: sin 50 ° = cos 40 °
Vì 40 ° < 50 ° nên cos 40 ° > cos 50 ° hay sin 50 ° > cos 50 °

a) Dùng bảng: sin 70 ° 13 ' ≈ 0 , 9410
- Cách nhấn máy tính:

b) cos 25 ° 32 ' ≈ 0 , 9023
- Cách nhấn máy tính:

c) t g 43 ° 10 ' ≈ 0 , 9380
- Cách nhấn máy tính:

d) c o t g 32 ° 15 ' ≈ 1 , 5850
- Cách nhấn máy tính:


sin 39 ° 13 ' ≈ 0,6323 cos 52 ° 18 ' ≈ 0,6115
tg 13 ° 20 ' ≈ 0,2370 cotg 10 ° 17 ' ≈ 0,5118
sin 45 ° ≈ 0,7071 cos 45 ° ≈ 0,7071
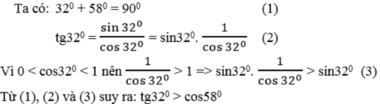
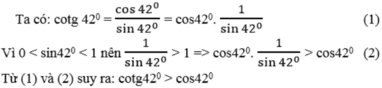


A B C D E
Để dễ hình dung, ta vẽ tam giác ABC vuông tại A, có DE là đường trung trực của cạnh BC ( D thuộc BC, E thuộc AC)
Giả sử góc C = 15 độ , độ dài đoạn AB = 1 (đvđd)
Ta có : Tam giác EBC cân tại E => Góc CBE = Góc C = 15 độ.
Ta có : Góc ABC = 75 độ => Góc ABE = 75 độ - 15 độ = 60 độ.
Suy ra EB = \(\frac{1}{Cos60}=2\) (đvđ.d) ; EA = \(Sin60.EB=\frac{\sqrt{3}}{2}.2=\sqrt{3}\)(đvđ.d) => AC = \(2+\sqrt{3}\)(đvđ.d)
Vì D là trung điểm BC nên ta có CD = DB = \(\frac{BC}{2}=\frac{\sqrt{AB^2+AC^2}}{2}=\frac{\sqrt{1^2+\left(2+\sqrt{3}\right)^2}}{2}=\sqrt{\frac{8+4\sqrt{3}}{4}}=\sqrt{2+\sqrt{3}}\) (đvđ.d)
\(Cos15=\frac{CD}{CE}=\frac{\sqrt{2+\sqrt{3}}}{2}=\frac{\sqrt{2}.\sqrt{4+2\sqrt{3}}}{4}=\frac{\sqrt{2}\left(\sqrt{3}+1\right)}{4}=\frac{\sqrt{6}+\sqrt{2}}{4}\)