Hai đội công nhân làm một đoạn đường. Đội 1 làm xong một nửa đoạn đường thì đội 2 đến làm tiếp nửa còn lại với thời gian nhiều hơn thời gian đội 1 làm là 28 ngày. Nếu hai đội cùng làm thì sau 45 ngày sẽ xong đoạn đường. Hỏi mỗi đội đã làm bao nhiêu ngày trên đoạn đường này?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi năng suất làm 1 ngày của đội 1, 2 lần lược là x, y (con đường/ ngày).
Thời gian đội 1 làm hết \(\frac{1}{2}\) con đường là: \(\frac{1}{2x}\)
Thời gian đội 2 làm hết \(\frac{1}{2}\) con đường là: \(\frac{1}{2y}\)
Theo đề bài ta có:
\(\frac{1}{2y}-\frac{1}{2x}=30\left(1\right)\)
Nếu hai đội cùng làm thì trong 72 ngày làm xong
\(\Rightarrow72x+72y=1\left(2\right)\)
Từ (1) và (2) ta có hệ: \(\hept{\begin{cases}\frac{1}{2y}-\frac{1}{2x}=30\\72x+72y=1\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=\frac{1}{120}\\y=\frac{1}{180}\end{cases}}\) (còn 1 nghiệm nữa mà loại rồi do nó âm)
Tới đây thì tự kết luận nha.

Gọi thời gian làm một mình của đội 1;đội 2 lần lượt là a,b
Theo đề, ta có: 1/a+1/b=1/36 và 2/3:1*b-1/3:1/a=40
=>\(\left\{{}\begin{matrix}\dfrac{1}{a}+\dfrac{1}{b}=\dfrac{1}{36}\\-\dfrac{1}{3}\cdot a+\dfrac{2}{3}\cdot b=40\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-a+2b=120\\\dfrac{1}{a}+\dfrac{1}{b}=\dfrac{1}{36}\end{matrix}\right.\)
=>a=2b-120 và \(\dfrac{1}{2b-120}+\dfrac{1}{b}=\dfrac{1}{36}\)
=>b+2b-120=1/36b(2b-120)
=>1/18b^2-10/3b-3b+120=0
=>1/18b^2-19/3b+120=0
=>b=90 hoặc b=24(loại)
=>a=2*90-120=180-120=60

Gọi số ngày đội một làm riêng để hoàn thành đoạn đường là x (ngày) (x>0)
số ngày đội hai làm riêng để hoàn thành đoạn đường là y (ngày) (y>0)
(x>y)
=> Trong một ngày đội một làm một mình được \(\frac{1}{x}\)(công việc)
Trong một ngày đội hai làm một mình được \(\frac{1}{y}\)(công việc)
Ta có hệ : \(\hept{\begin{cases}\frac{1}{x}+\frac{1}{y}=\frac{1}{48}\\\frac{1}{2}x+\frac{1}{2}y=100\end{cases}}\)
Giải ra được x = 120 ; y = 80 (vì x>y)
Vậy : Nếu làm riêng thì đội một phải làm trong 120 ngày mới xong đoạn đường; đội hai phải làm trong 80 ngày mới xong đoạn đường

Gọi x là công suất của đội 1 làm được trong 1 ngày, y là công suất của đội 2 làm được trong 1 ngày
Ta có phương trình: 5x=3.(x+y)\(\Rightarrow\)5x=3x+3y\(\Rightarrow\)2x=3y\(\Rightarrow\)x=\(\frac{3}{2}\)y
\(\Rightarrow\)Ta có phương trình: \(\frac{3}{2}\)y.10=y.Thời gian đội công nhân 2 làm cả đoạn đường
\(\Rightarrow\)Thời gian đội công nhân 2 làm cả đoạn đường=15
\(Đáp\) \(số:15\) \(ngày\)

Gọi a(ngày) và b(ngày) lần lượt là thời gian mỗi đội công nhân hoàn thành công việc khi làm riêng(Điều kiện: a>6; b>6)
Trong 1 ngày, đội 1 làm được: \(\dfrac{1}{a}\)(công việc)
Trong 1 ngày, đội 2 làm được: \(\dfrac{1}{b}\)(công việc)
Trong 1 ngày, hai đội làm được: \(\dfrac{1}{6}\)(công việc)
Do đó, ta có phương trình: \(\dfrac{1}{a}+\dfrac{1}{b}=\dfrac{1}{6}\)(1)
Vì khi đội 1 làm 3 ngày và đội 2 làm 7 ngày thì chỉ làm được 2/3 công việc nên ta có phương trình:
\(\dfrac{3}{a}+\dfrac{7}{b}=\dfrac{2}{3}\)(2)
Từ (1) và (2) ta lập được hệ phương trình:
\(\left\{{}\begin{matrix}\dfrac{1}{a}+\dfrac{1}{b}=\dfrac{1}{6}\\\dfrac{3}{a}+\dfrac{7}{b}=\dfrac{2}{3}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{3}{a}+\dfrac{3}{b}=\dfrac{1}{2}\\\dfrac{3}{a}+\dfrac{7}{b}=\dfrac{2}{3}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{-4}{b}=-\dfrac{1}{6}\\\dfrac{1}{a}+\dfrac{1}{b}=\dfrac{1}{6}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=24\\\dfrac{1}{a}=\dfrac{1}{6}-\dfrac{1}{24}=\dfrac{1}{8}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=8\\b=24\end{matrix}\right.\)(thỏa ĐK)
Vậy: Khi làm riêng thì đội 1 cần 8 ngày để hoàn thành công việc
Khi làm riêng thì đội 2 cần 24 ngày để hoàn thành công việc
Gọi thời gian đội 1 làm một mình xong công việc là x (x>6)
Gọi thời gian đội 2 làm một mình xong công việc là y (y>6)
Trong 1 ngày:
-Đội 1 làm một mình được: \(\dfrac{1}{x}\) công việc
-Đội 2 làm một mình được: \(\dfrac{1}{y}\) công việc
-Cả 2 đội làm được : \(\dfrac{1}{6}\) công việc
Ta có PT: \(\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{6}\) (1)
-Nếu đội 1 làm 3 ngày và đội 2 làm 7 ngày thì chỉ được 2/3 công việc nên ta có PT: \(\dfrac{3}{x}+\dfrac{7}{y}=\dfrac{2}{3}\) (2)
Từ (1) và (2) ta có HPT: \(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{6}\\\dfrac{3}{x}+\dfrac{7}{y}=\dfrac{2}{3}\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}x=8\\y=24\end{matrix}\right.\left(TM\right)\)
Vậy đội 1 làm một mình trong 8 giờ thì xong công việc
Vậy đội 2 làm một mình trong 24 giờ thì xong công việc

Gọi x (ngày) là thời gian đội thứ nhất làm riêng xong nửa công việc.
Điều kiện: 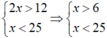 ⇒ 6 < x < 25
⇒ 6 < x < 25
Khi đó thời gian làm riêng xong nửa công việc của đội thứ hai là: 25 – x (ngày)
trong 1 ngày, đội thứ nhất làm được 1/2x (công việc)
trong 1 ngày, đội thứ hai làm được 1/[2.(25 - x)] (công việc)
trong 1 ngày, cả hai đội làm được 1/12 (công việc)
Theo đề bài, ta có phương trình:
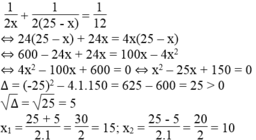
Cả hai giá trị của x đều thỏa mãn điều kiện bài toán
Vậy đội thứ nhất làm riêng xong công việc trong 15.2 = 30 ngày
đội thứ hai làm riêng xong công việc trong 20 ngày
hoặc đội thứ nhất làm riêng xong công việc trong 10.2 = 20 ngày
đội thứ hai làm riêng xong công việc trong 30 ngày.
Gọi tg đội là a,b(a,b>0)
1 ngày đội 1 làm đc: 1/a (đoạn đường)
1 ngày đội 2 làm đc: 1/b (đoạn đường)
Theo bài ra ta có:
1 ngày cả 2 đội làm đc: 1/45=1/45 (đoạn đường)
=> 1/a + 1/b=1/45 (1)
Đội 1 làm xong 1 nửa đoạn đường thì đội 2 làm nốt 1 nửa với thời gian nhiều hơn đội 1 là 28 ngày
=>.b/2 - a/2 = 28
=> b-a = 56 => b = a+ 56 (2)
Thay (2) vào (1) ta có:
1/a + 1/(a+56) = 1/45 (*)
Giải (*) ta đc: a=......
=> 1/b= 1/... - 1/.......=1/....
=>. b=........