Cho tam giác ABC có a=8m,b=10m,c=12m
a,Tính nửa chu vi p
b,TÍnh diện tích S của tam giác ABC
c,Tính góc A của tam giác ABC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(p=\dfrac{a+b+c}{2}=15\)
\(S=\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}=\sqrt{15\left(15-8\right)\left(15-10\right)\left(15-12\right)}=15\sqrt{7}\)
\(cosA=\dfrac{b^2+c^2-a^2}{2bc}=\dfrac{10^2+12^2-8^2}{2.10.12}=\dfrac{3}{4}\Rightarrow A\approx41^024'\)

a. + CH = 10 - 3.6 = 6.4 (cm)
- Áp dụng hệ thức về cạnh và đường cao trong tam giác vuông vào ΔABC ta có :
+ \(AH^2=BH.CH\)
\(\Rightarrow AH=\sqrt{BH.CH}=\sqrt{3,6.6,4}=4.8\) (cm)
+ \(AB^2=BC.BH\)
\(\Rightarrow AB=\sqrt{BC.BH}=\sqrt{10.3,6}=6\) (cm)
+ \(AC^2=BC.CH\)
\(\Rightarrow AC=\sqrt{BC.CH}=\sqrt{10.6,4}=8\) (cm)
b. \(S_{ABC}=\dfrac{1}{2}.AB.AC=\dfrac{1}{2}.6.8=24\left(cm^2\right)\)
c. \(P_{ABC}=AB+AC+BC=6+8+10=24\left(cm\right)\)

a) Áp dụng định lí cosin, ta có:
\(\begin{array}{l}{a^2} = {b^2} + {c^2} - 2bc.\cos A\\ \Leftrightarrow {a^2} = {8^2} + {5^2} - 2.8.5.\cos {120^ \circ } = 129\\ \Rightarrow a = \sqrt {129} \end{array}\)
Áp dụng định lí sin, ta có:
\(\begin{array}{l}\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} \Rightarrow \frac{{\sqrt {129} }}{{\sin {{120}^ \circ }}} = \frac{8}{{\sin B}} = \frac{5}{{\sin C}}\\ \Rightarrow \left\{ \begin{array}{l}\sin B = \frac{{8.\sin {{120}^ \circ }}}{{\sqrt {129} }} \approx 0,61\\\sin C = \frac{{5.\sin {{120}^ \circ }}}{{\sqrt {129} }} \approx 0,38\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\widehat B \approx 37,{59^ \circ }\\\widehat C \approx 22,{41^ \circ }\end{array} \right.\end{array}\)
b) Diện tích tam giác ABC là: \(S = \frac{1}{2}bc.\sin A = \frac{1}{2}.8.5.\sin {120^ \circ } = 10\sqrt 3 \)
c)
+) Theo định lí sin, ta có: \(R = \frac{a}{{2\sin A}} = \frac{{\sqrt {129} }}{{2\sin {{120}^ \circ }}} = \sqrt {43} \)
+) Đường cao AH của tam giác bằng: \(AH = \frac{{2S}}{a} = \frac{{2.10\sqrt 3 }}{{\sqrt {129} }} = \frac{{20\sqrt {43} }}{{43}}\)

Bổ sung đề: \(\widehat{B}=30^0\)
a) Xét ΔABC vuông tại A có \(\widehat{B}=30^0\)(gt)
mà cạnh đối diện với \(\widehat{B}\) là cạnh AC
nên \(AC=\dfrac{1}{2}\cdot BC\)(Định lí tam giác vuông)
\(\Leftrightarrow AC=\dfrac{1}{2}\cdot7=\dfrac{7}{2}cm\)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow AB^2=7^2-\left(\dfrac{7}{2}\right)^2=\dfrac{147}{4}\)
hay \(AB=\dfrac{7\sqrt{3}}{2}cm\)
Vậy: AC=3,5cm; \(AB=\dfrac{7\sqrt{3}}{2}cm\)

Gợi ý thôi nhé.
a) Có \(AB=\sqrt{\left(x_B-x_A\right)^2+\left(y_B-y_A\right)^2}=\sqrt{\left(\left(-1\right)-6\right)^2+\left(2-\left(-1\right)\right)^2}=\sqrt{58}\)
Tương tự như vậy, ta tính được AC, BC.
Tính góc: Dùng \(\cos A=\dfrac{AB^2+AC^2-BC^2}{2AB.AC}\)
b) Chu vi thì bạn lấy 3 cạnh cộng lại.
Diện tích: Dùng \(S_{ABC}=\dfrac{1}{2}AB.AC.\sin A\)
c) Gọi \(H\left(x_H,y_H\right)\) là trực tâm thì \(\left\{{}\begin{matrix}AH\perp BC\\BH\perp AC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\overrightarrow{AH}.\overrightarrow{BC}=0\\\overrightarrow{BH}.\overrightarrow{AC}=0\end{matrix}\right.\)
Sau đó dùng: \(\overrightarrow{u}\left(x_1,y_1\right);\overrightarrow{v}\left(x_2,y_2\right)\) thì \(\overrightarrow{u}.\overrightarrow{v}=x_1x_2+y_1y_2\) để lập hệ phương trình tìm \(x_H,y_H\)
Trọng tâm: Gọi \(G\left(x_G,y_G\right)\) là trọng tâm và M là trung điểm BC. Dùng \(\left\{{}\begin{matrix}x_M=\dfrac{x_B+x_C}{2}\\y_M=\dfrac{y_B+y_C}{2}\end{matrix}\right.\) để tìm tọa độ M.
Dùng \(\overrightarrow{AG}=\dfrac{2}{3}\overrightarrow{AM}\) để lập hpt tìm tọa độ G.

a) + Δ ABC vuông tại A, có 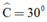
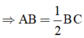
(Trong một tam giác vuông, cạnh đối diện với góc 30o bằng một nửa cạnh huyền)
+ Δ ABC có BD là phân giác của 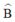
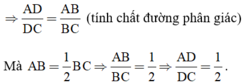
b) AB = 12,5cm ⇒ BC = 2AB = 2.12,5 = 25cm
Áp dụng định lí Py- ta- go vào tam giác ABC ta có:
AB2 + AC2 = BC2 nên AC2 = BC2 - AB2
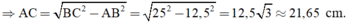
+ Chu vi tam giác ABC là:
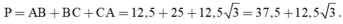
+ Diện tích tam giác ABC là:
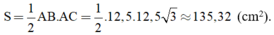

Tổng độ dài hai cạnh AB và AC là :
24 - 10 = 14 ( cm )
Độ dài cạnh AB là :
14 : ( 3 + 4 ) x 3 = 6 ( cm )
Độ dài cạnh AC là :
14 - 6 = 9 ( cm )
Diện tích hình tam giác ABC là :
6 x 9 : 2 = 27 ( cm2)
Đáp số : 27 cm2
tổng độ dài hai cạnh là
24-10=14 cm
độ dại cạnh AB là
14:(3+4).3=6 cm
độ dài cạnh AC là
14-6=8 cm
diện tích là
6.7:2=27cm2
đáp số...............


* Cách vẽ:
- Kẻ tỉa Ax bất kì khác tia AB, AC
- Trên tia Ax, lấy hai điểm E và F sao cho AE = 2 (đơn vị dài), EF = 3 (đơn vị dài)
- Kẻ đường thẳng FB
- Từ E kẻ đường thẳng song song với FB Cắt AB tại M.
- Kẻ đường thẳng FC.
- Từ E kẻ đường thẳng song song với FC cắt AC tại N.
Ta có M, N là hai điểm cần vẽ.
* Chứng minh:
Gọi p' và S' là chu vi và diện tích của △ AMN.
Trong △ ABC, ta có: MN // BC
Suy ra: △ AMN đồng dạng ΔABC
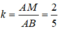
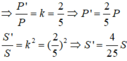

Bài 1:
a: AB+AC=75-45=30(cm)
b: AB=(30+4):2=17(cm)
=>AC=13cm
\(S=17\cdot13=221\left(cm^2\right)\)
Bài 2:
a: BC=67-47=20(cm)
b: \(S=\dfrac{15\cdot20}{2}=15\cdot10=150\left(cm^2\right)\)