Giúp e với bài hình với 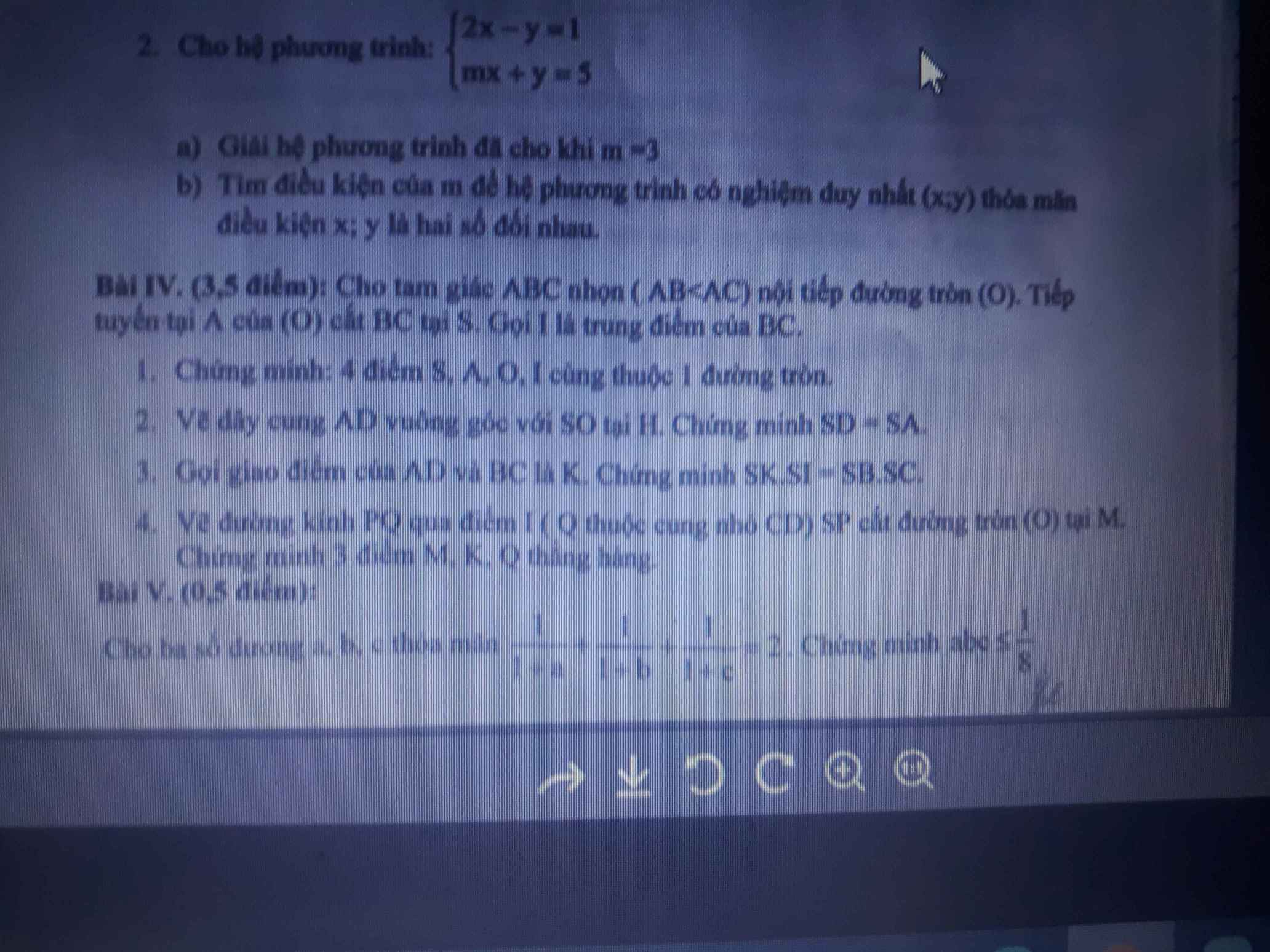
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a: Xét ΔHAC vuông tại H và ΔABC vuông tại A có
\(\widehat{C}\) chung
Do đó: ΔHAC~ΔABC
b: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=15^2+20^2=625\)
=>BC=25
Xét ΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}BH\cdot BC=BA^2\\AH\cdot BC=AB\cdot AC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH\cdot25=15^2=225\\AH\cdot25=15\cdot20=300\end{matrix}\right.\)
=>BH=9; AH=12

a: Xét ΔADE vuông tại E và ΔCBF vuông tại F có
AD=BC
\(\widehat{ADE}=\widehat{CBF}\)
Do đó: ΔADE=ΔCBF
Suy ra: AE=CF
Xét tứ giác AECF có
AE//CF
AE=CF
Do đó: AECF là hình bình hành
b: Xét tứ giác AICK có
AI//CK
AK//IC
Do đó: AICK là hình bình hành
Suy ra: AI=CK
c: Ta có: ΔADE=ΔCBF
nên DE=BF

Bài 1:
a: \(36a^4-y^2=\left(6a^2-y\right)\left(6a^2+y\right)\)
n: \(6x^2+x-2\)
\(=6x^2+4x-3x-2\)
\(=\left(3x+2\right)\left(2x-1\right)\)

Bài 2:
a: Xét ΔBDC có
M là trung điểm của BC
ME//BD
Do đó: E là trung điểm của DC
Suy ra: DE=EC(1)
Xét ΔAME có
I là trung điểm của AM
ID//ME
Do đó: D là trung điểm của AE
Suy ra: AD=DE(2)
Từ (1) và (2) suy ra AD=DE=EC

Bài 2:
Ta có: \(3n^3+10n^2-5⋮3n+1\)
\(\Leftrightarrow3n^3+n^2+9n^2+3n-3n-1-4⋮3n+1\)
\(\Leftrightarrow3n+1\in\left\{1;-1;2;-2;4;-4\right\}\)
\(\Leftrightarrow3n\in\left\{0;-3;3\right\}\)
hay \(n\in\left\{0;-1;1\right\}\)

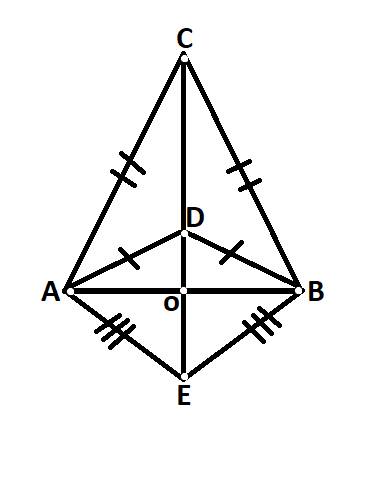
CA=CB
DA=DB
Do đó: CD là trung trực của BA(1)
EA=EB
=>E nằm trên trung trực của AB(2)
Từ (1), (2) suy ra C,D,E thẳng hàng

2.1
ĐKXĐ: \(x\ge-\dfrac{1}{16}\)
\(x^2-x-20-2\left(\sqrt{16x+1}-9\right)=0\)
\(\Leftrightarrow\left(x-5\right)\left(x+4\right)-\dfrac{32\left(x-5\right)}{\sqrt{16x+1}+9}=0\)
\(\Leftrightarrow\left(x-5\right)\left(x+4-\dfrac{32}{\sqrt{16x+1}+9}\right)=0\) (1)
Do \(x\ge-\dfrac{1}{16}\Rightarrow\left\{{}\begin{matrix}\dfrac{32}{\sqrt{16x+1}+9}< \dfrac{32}{9}\\x+4\ge-\dfrac{1}{16}+4=\dfrac{63}{16}>\dfrac{32}{9}\end{matrix}\right.\)
\(\Rightarrow x+4-\dfrac{32}{\sqrt{16x+1}+9}>0\)
Nên (1) tương đương:
\(x-5=0\)
\(\Leftrightarrow x=5\)
Câu 2.2, 2.3 đề lỗi không dịch được








b)
Để hệ có nghiệm duy nhất \(\Leftrightarrow m\ne-2\)
Khi đó \(\left\{{}\begin{matrix}2x-y=1\\mx+y=5\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}2x-y=1\\\left(m+2\right)x=6\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=\frac{6}{m+2}\\y=2x-1=\frac{10-m}{m+2}\end{matrix}\right.\)
Để x;y là 2 số đối nhau \(\Leftrightarrow x+y=0\)
\(\Leftrightarrow\frac{6}{m+2}+\frac{10-m}{m+2}=0\Rightarrow16-m=0\Rightarrow m=16\)