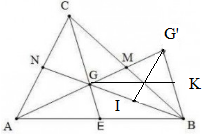
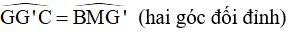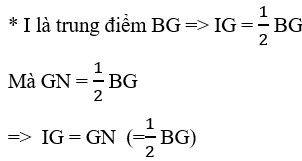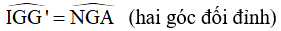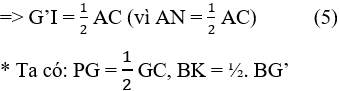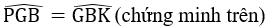bài 2: gọi G là trọng tâm của tam giác ABC.trên tia AG lấy điểm G' sao cho G là trung điểm của AG'
a)so sánh các cạnh của tam giác BGG' với các đường trung tuyến của tam giác ABC
b) so sánh các đường trung tuyến của tam giác BGG' với các cạnh của tam giác ABC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
19 tháng 4 2017
Hướng dẫn:
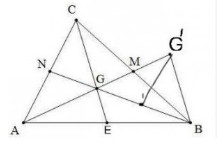
a) So sánh các cạnh của ∆BGG’ với các đường trung tuyến của ∆ABC BG cắt AC tại N
CG cắt AB tại E
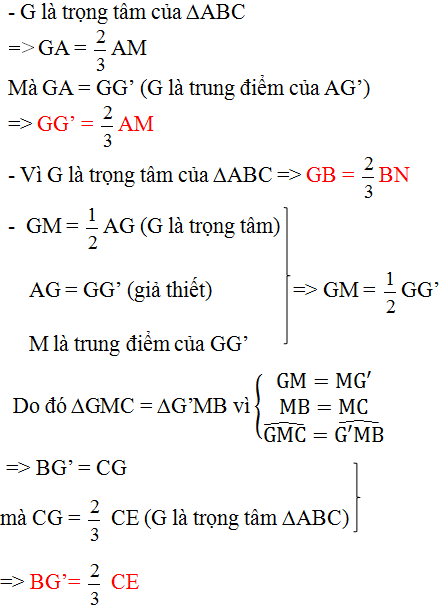
G là trọng tâm của ∆ABC
=> GA = 
AM
Mà GA = GG’ ( G là trung điểm của AG ‘)
GG’ = AM
Vì G là trọng tâm của ∆ABC => GB = BN
Mặt khác : GM = 
AG ( G là trọng tâm )
AG = GG’ (gt)
GM = GG’
M là trung điểm GG’
Do đó ∆GMC = ∆G’MB vì :
GM = MG’
MB = MC
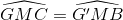
=> BG' = CG
mà CG = CE (G là trọng tâm ∆ABC)
=> BG' = CE
Vậy mỗi cạnh của ∆BGG' bằng đường trung tuyến của ∆ABC
b) So sánh các đường trung tuyến của ∆BGG' với cạnh ∆ABC
ta có: BM là đường trung tuyến ∆BGG'
mà M là trung điểm của BC nên BM = BC
Vì IG = BG (I là trung điểm BG)
GN = BG ( G là trọng tâm)
=> IG = GN
Do đó ∆IGG' = ∆NGA (cgc) => IG' = AN => IG' =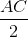 
- Gọi K là trung điểm BG => GK là trung tuyến ∆BGG'
Vì GE = GC (G là trọng tâm ∆ABC)
=> GE = BG
mà K là trung điểm BG' => KG' = EG
Vì ∆GMC = ∆G'BM (chứng minh trên)
=> 
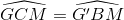(lại góc sole trong)
=> CE // BG' =>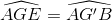 
(đồng vị)
Do đó ∆AGE = ∆GG'K (cgc) => AE = GK
mà AE = AB nên GK = AB
Vậy mỗi đường trung tuyến ∆BGG' bằng một nửa cạnh của tam giác ABC song song với nó
19 tháng 4 2017
Hướng dẫn làm bài:
a)So sánh các cạnh của ∆BGG’ với các đường trung tuyến của ∆ABC
BG cắt AC tại N
CG cắt AB tại E
G là trọng tâm của ∆ABC
=> GA=23AMGA=23AM
Mà GA = GG’ (G là trung điểm của AG’)
=> GG′=23AMGG′=23AM
Vì G là trọng tâm của ∆ABC => GB=23BNGB=23BN
Mặt khác :
M là trung điểm GM=12AG(TT)AG=GG′(Gt)}=>GM=12GG′GM=12AG(TT)AG=GG′(Gt)}=>GM=12GG′
Do đó ∆GMC=∆G’MB vì ⎧⎪⎨⎪⎩GM=MG′MB=MCˆGMC=ˆG′MB{GM=MG′MB=MCGMC^=G′MB^
=> BG′=CGCG=23CEBG′=CGCG=23CE (G là trọng tâm tam giác ABC)
=>BG′=23CE=>BG′=23CE
Vậy mỗi cạnh của ∆BGG’ bằng 2323 đường trung tuyến của ∆ABC
b)So sánh các đường trung tuyến của ∆BGG’ với cạnh ∆ABC.
-Ta có: BM là đường trung tuyến ∆BGG’
Mà M là trung điểm của BC nên BM=12BCBM=12BC
Vì IG=12BGIG=12BG (Vì I là trung điểm BG)
GN=12BGGN=12BG (G là trọng tâm)
=> IG = GN
Do đó ∆IGG’=∆NGA (c.g.c) => IG′=AN=>IG′=AC2IG′=AN=>IG′=AC2
-Gọi K là trung điểm BG => GK là trung điểm ∆BGG’
Vì GE=12GCGE=12GC (G là trọng tâm tam giác ABC)
BG' = GC (Chứng minh trên)
=>GE=12BG=>GE=12BG
Mà K là trung điểm BG’ =>KG’ = EG
Vì ∆GMC = ∆G’MB (chứng minh trên)
=> ˆGCM=ˆG′BMGCM^=G′BM^ (So le trong)
=>CE // BG’ => ˆAGE=ˆAG′BAGE^=AG′B^ (đồng vị)
Do đó ∆AGE = ∆GG’K (c.g.c) =>AE = GK
Mà AE=12AB⇒GK=12AB
WH
6 tháng 3 2018
Bài giải
a) Gọi M, N, E lần lượt là trung điểm của AB, BC, CA.
Vậy mỗi cạnh của ΔBGG' bằng 2/3 đường trung tuyến của ΔABC.
b) Gọi I, K lần lượt là trung điểm của BG và BG'.
Vậy mỗi đường trung tuyến của ΔBGG' bằng một nửa cạnh của ΔABC tương ứng với nó.~Hok tốt~
TV
1 tháng 4 2016
gọi tam giác ABC có các đường trung tuyến là AI, BH, CF
a, nhận xét: ta thấy tam giác BGG' có các cạnh =2/3 các trung tuyến của tam giác ABC theo các cặp tương ứng
BG=2/3BH , BG'=2/3CF , GG'=2/3AI
chưng minh:
ta có :
*BG=2/3BH theo tính chất đường trung tuyến
* xét tứ giác BGCG' có
- I là trung điểm của BC ( theo giả thiết)
- I là trung điểm của GG'
VÌ: GG'=AG
GI=1/2AG
=> GI =1/2GG'
=> I là trung điểm của GG'
=>tứ giác BGCG' là hình thoi
=>BG'=GC
=>BG'=2/3CF
*như chứng minh trên ta có
AG=GG'
mà AG=2/3AI
=> GG'=2/3AI
=> ĐIỀU CẦN CHỨNG MINH
b,gọi các điểm J,K lằn lượt là trung điểm của BG, BG'
nhận xét; ta thấy các đường trung tuyến của BGG'=1/2 các cạnh của ABC tương ứng
*BI=1/2BC( gia thuyết)
*cm:GK=1/2AB
xét tam gác ABG'
G là trung điểm của AG'
K là trung điểm của BG'
=> GK=1/2AB (tính chất đường trung tuyến)
*cm; G'J=1/2AC
GH=1/2BG
JG=1/2BG
=>GH=JG
GA=GG'(giả thuyết)
=> tứ giác AJG'H là hình thoi
=> JG'=AH
AH=1/2AC
=>JG'=1/2AC
điều phải chứng minh
TV
1 tháng 4 2016
a) So sánh các cạnh của tam giác BGG' với các đường trung tuyến của tam giác ABC:
gọi M;N;P là trung điểm của BC; AC; AB
cạnh của tam giác BGG" là:
BG = 2/3.BN
GG' = AG = 2/3.AM
BG' =- CG = 2/3.CP ( do tam giác BG'M = CMG => BG'=CG)
b) So sánh các đường trung tuyến của tam giác BGG' với các cạnh của tam giác ABC:
Gọi I là trung điểm GG', K là trung điểm BG
BM = BC/2
GI = AB/2 ( AG là đường trung bình của tam giác BGG')
G'K = AN = AC/2 ( tg ANG= tgG'GK => G'K= AN)
2 tháng 5 2019
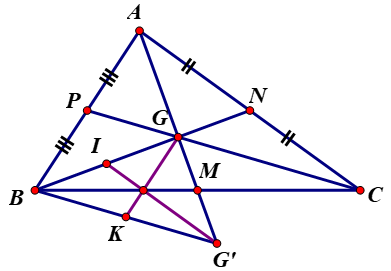
a) Gọi trung điểm BC, CA, AB lần lượt là M, N, P.
⇒ AM, BN, CP là các đường trung tuyến, G là trọng tâm của ΔABC
Theo tính chất đường trung tuyến của tam giác ta có:
GB = 2/3.BN (1)
GA = 2/3.AM, mà GA = GG’ (do G là trung điểm của AG’) ⇒ GG’ = 2/3.AM (2)
GM=1/2.AG, mà AG=GG’ ⇒ GM=1/2.GG’ ⇒ M là trung điểm của GG’ hay GM = GM’ .
Xét ΔGMC và ΔG’MB có:
GM = G’M (chứng minh trên)
MC = MB
⇒ ΔGMC = ΔG’MB (c.g.c)
⇒ GC = G’B (hai cạnh tương ứng).
Mà CG = 2/3.CP (tính chất đường trung tuyến) ⇒ G’B = 2/3.CP (3)
Từ (1), (2), (3) ta có : GG’ = 2/3.AM , GB = 2/3.BN, G’B = 2/3.CP.
2 tháng 5 2019
b) Gọi I, K lần lượt là trung điểm của BG, BG’.
* M là trung điểm GG’⇒ BM là đường trung tuyến ΔBGG.
Mà M là trung điểm BC ⇒ BM = ½ .BC (4)
Xét ΔIGG’ và ΔNGA có:
IG = GN (chứng minh trên)
GG’ = GA (Vì G là trung điểm AG’)
⇒ ΔIGG’ = ΔNGA (c.g.c)
⇒ G’I = AN (hai cạnh tương ứng)
Mà GC = BG’ (chứng minh phần a))
⇒ Nên PG = BK.
ΔGMC = ΔG’MB (chứng minh câu a)
Xét ΔPGB và ΔKBG có:
PG = BK (chứng minh trên)
BG chung
⇒ ΔPGB = ΔKBG (c.g.c)
⇒ PB = GK (hai cạnh tương ứng)
28 tháng 3 2019
a) So sánh các cạnh của ∆BGG’ với các đường trung tuyến của ∆ABC.
Gọi M, N, E lần lượt là trung điểm của BC, CA, AB.
- G là trọng tâm của ∆ABC
⇒⇒ GA = \(\frac{2}{3}\) AM
Mà GA = GG’ (G là trung điểm của AG’)
⇒⇒ GG' = \(\frac{2}{3}\) AM
- Vì G là trọng tâm của ∆ABC ⇒⇒ GB = \(\frac{2}{3}\) BN
- Ta có:
GM = \(\frac{1}{2}\) AG (do G là trọng tâm) và AG = GG' (gt)
⇒⇒ GM = \(\frac{1}{2}\) GG'
Xét ∆GMC và ∆G’MB có:
GM = MG'
MB = MC
ˆGMC=ˆG′MBGMC^=G′MB^ (hai góc đối đỉnh)
Vậy ∆GMC=∆G’MB.
⇒⇒ BG' = CG
Mà CG = \(\frac{2}{3}\) CE (G là trọng tâm tam giác ABC)
⇒⇒ BG' = \(\frac{2}{3}\) CE
Vậy mỗi cạnh của ∆BGG’ bằng \(\frac{2}{3}\) đường trung tuyến của ∆ABC.
28 tháng 3 2019
b) So sánh các đường trung tuyến của ∆BGG’ với các cạnh của ∆ABC.
- Ta có: BM là đường trung tuyến ∆BGG’
Mà M là trung điểm của BC nên BM = \(\frac{1}{2}\) BC
Vì IG = \(\frac{1}{2}\) BG (Do I là trung điểm BG)
GN = \(\frac{1}{2}\) BG (G là trọng tâm)
⇒⇒ IG = GN
Xét ∆IGG’ và ∆NGA có:
IG = GN (cmt)
GG' = GA (gt)
ˆIGG′=ˆNGAIGG′^=NGA^ (hai góc đối đỉnh)
Vậy ∆IGG’ = ∆NGA (c.g.c) ⇒ IG' = AN ⇒ IG' = AC2AC2
- Gọi K là trung điểm BG ⇒ GK là trung tuyến của ∆BGG’
Vì GE = \(\frac{1}{2}\) GC (G là trọng tâm tam giác ABC)
BG' = GC (cmt)
⇒⇒ GE =\(\frac{1}{2}\) BG'
Mà K là trung điểm BG’ ⇒⇒ KG’ = EG
Vì ∆GMC = ∆G’MB (cmt)
⇒⇒ ˆGCM=ˆG′BMGCM^=G′BM^ (hai góc tương ứng)
⇒⇒ CE // BG’ ⇒ ˆAGE=ˆAG′BAGE^=AG′B^ (đồng vị)
Xét ∆AGE và ∆GG’K có:
EG = KG’ (cmt)
AG = GG' (gt)
ˆAGE=ˆAG′BAGE^=AG′B^ (cmt)
Vậy ∆AGE = ∆GG’K (c.g.c) ⇒⇒ AE = GK
Mà AE = \(\frac{1}{2}\) AB ⇒⇒ GK = \(\frac{1}{2}\) AB
Vậy mỗi đường trung tuyến của ∆BGG’ bằng một nửa cạnh của tam giác ABC song song với nó