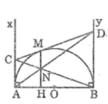
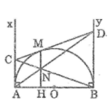
Cho nửa đường tròn tâm O, đường kính AB. Trên tiếp tuyến thuộc nửa đường tròn bờ là AB, lấy D sao cho AD > R. Kẻ tiếp tuyến DC ( C khác A), hạ đường cao CH, H thuộc AB. Chứng minh giao điểm của DB và CH là trung điểm của CH.
P/s: mn giúp với, nghĩ mãi k ra cay quá

Cô hướng dẫn em nhé ^^ Suy nghĩ một chút là ra ý mà :)
Gọi E là giao điểm của BC và AD, I là giáo điểm của CH và DB.
Đầu tiên, ta chứng minh DE=DC. Thật vậy, ta thấy ngay góc DCE= góc HCB (Cùng phụ góc ABC ). Mà gócDEC = góc HCB nên góc DEC = góc DCE hay tam giác DEC cân tại D, vậy DE=DC. Lại có DC =DA nên DA =DE.
Do CH song song AE, áp dụng Ta let:
\(\frac{IH}{DA}=\frac{BI}{BD}=\frac{IC}{DE}\) . Do DA = DE nên IH = IC.
Chúc em học tốt ^^