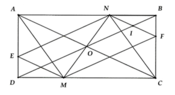
Cho hình bình hành \(ABCD\), kẻ đường thẳng đi qua \(D\) cắt AB ở \(M\), cắt \(BC\) ở \(N\), cắt \(AC\) ở \(I\).
a) Chứng minh: \(\dfrac{AM}{AB}=\dfrac{CB}{CN}=\dfrac{DM}{DN}\) Từ đó suy ra \(AM.CN\) không đổi.
b) Chứng minh: \(ID^2 = IM.IN\)
c) Vẽ \(Bx//AC\), \(Bx\) cắt \(MN\) tại \(E\). Chứng minh: \(\dfrac{EM}{EN}=\dfrac{DM}{DN}\)
d) Lấy \(K\) bất kỳ trên cạnh \(CD\). \(KI\) và \(KN\) cắt \(AB\) ở \(P\) và \(Q\). Chứng minh: \(\dfrac{MP}{MQ}=\dfrac{MA}{MB}\)