Cho 2 đ.tròn (O)và(O') cắt nhau tại 2 điểm AvàB . Kẻ đường kính AOC và AO'D,một cát tuyến của B cắt hai đ.tròn này tại MvàN MC cắt ND tại I(M∈(O);N∈(o')),ND tại I
CM:Các góc MACvàNAD bằng nhau và suy ra tứ giác ACID nội tiếp
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

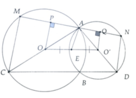
a, Chú ý: C M A ^ = D N A ^ = 90 0
b, Vẽ OP ⊥ MA; O'Q ⊥ NA
Chú ý hình thang vuông OPQO’ có EA là đường trung bình

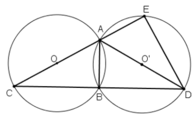
Vì A,B,C ∈ (O)
⇒ BO = OA = OC
⇒ BO = AC/2.
Tam giác ABC có đường trung tuyến BO và BO bằng một phần hai độ dài cạnh tương ứng AC
=> Tam giác ABC là tam giác vuông tại B ( định lí)
⇒ 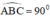
Chứng minh tương tự
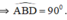
Đường tròn tâm O và O’ bằng nhau ⇒ AC = AD.(AC,AD lần lượt là bán kính của (O) và (O’))
Xét hai tam giác vuông ΔABC và ΔABD có:
AB chung, AC = AD
⇒ ΔABC = ΔABD (cạnh huyền – cạnh góc vuông)
⇒ BC = BD(hai cạnh tương ứng)
⇒ 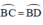 ( định lý )
( định lý )

Có phải cát tuyến của hai đường tròn đi qua A không bạn nhỉ?