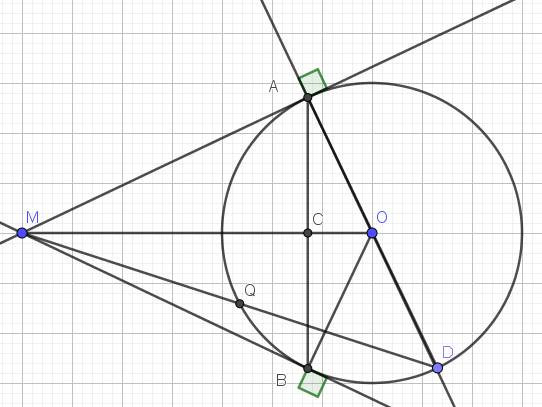
Từ một điểm A nằm ngoài đường tròn tâm O, bán kính R (AO < 2R) vẽ hai tiếp tuyến AD, AE với (O) (D,E là các tiếp điểm).Gọi H là giao điểm của DE và AO.Lấy điểm M thuộc cung nhỏ DE (M khác D khác E, MD < ME).Tia AM cắt đường tròn (O;R) tại N.Đoạn thẳng AO cắt cung nhỏ DE tại K.
a) Chứng minh AO vuông góc với DE và AD2 = AM.AN
b) Chứng minh NK là tia phân giác của góc DNI và tứ giác MHON nội tiếp.
c) Kẻ đường kính KQ của đường tròn (O;R).Tia QN cắt tia ED tại C.Chứng minh MD.CE = ME.CD
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác MAOB có
\(\widehat{MAO}+\widehat{MBO}=90^0+90^0=180^0\)
=>MAOB là tứ giác nội tiếp
=>M,A,O,B cùng thuộc một đường tròn
b: Xét (O) có
MA,MB là các tiếp tuyến
Do đó: MA=MB
=>M nằm trên đường trung trực của AB(1)
Ta có: OA=OB
=>O nằm trên đường trung trực của BA(2)
Từ (1) và (2) suy ra MO là đường trung trực của BA
=>MO\(\perp\)BA tại C và C là trung điểm của AB
Xét ΔMAO vuông tại A có AC là đường cao
nên \(MC\cdot MO=MA^2\left(3\right)\)
Xét (O) có
ΔAQD nội tiếp
AD là đường kính
Do đó: ΔAQD vuông tại Q
=>QA\(\perp\)QD tại Q
=>AQ\(\perp\)DM tại Q
Xét ΔADM vuông tại A có AQ là đường cao
nên \(MQ\cdot MD=MA^2\left(4\right)\)
Từ (3) và (4) suy ra \(MC\cdot MO=MQ\cdot MD\)

a: ΔODE cân tại O
mà OM là trung tuyến
nên OM vuông góc DE
=>góc OMA=90 độ=góc OCA=góc OBA
=>O,A,B,M,C cùng thuộc 1 đường tròn
b: Xét ΔBSC và ΔCSD có
góc SBC=góc SCD
góc S chung
=>ΔBSC đồng dạng với ΔCSD
=>SB/CS=SC/SD
=>CS^2=SB*SD
góc DAS=gócEBD
=>góc DAS=góc ABD
=>ΔSAD đồng dạng với ΔSBA
=>SA/SB=SD/SA
=>SA^2=SB*SD=SC^2
=>SA=SC
c; BE//AC
=>EH/SA=BH/SC=HJ/JS
mà SA=SC
nênHB=EH
=>H,O,C thẳng hàng

Lời giải:
1. Vì $MA, MB$ là tiếp tuyến của $(O)$ nên $MA\perp OA, MB\perp OB$.
Khi đó $\widehat{MAO}=\widehat{MBO}=90^0$
Tứ giác $MAOB$ có tổng 2 góc đối nhau $\widehat{MAO}+\widehat{MBO}=90^0+90^0=180^0$
$\Rightarrow MAOB$ là tứ giác nội tiếp.
$\Rightarrow M,A,O,B$ cùng thuộc 1 đường tròn.
2.
Có: $MA=MB, OA=OB$ nên $MO$ là trung trực của $AB$
$\Rightarrow MO\perp AB$ tại $C$.
Xét tam giác $MOB$ vuông tại $B$ có đường cao $BC$. Áp dụng hệ thức lượng trong tam giác vuông thì:
$MC.MO=MB^2(1)$
Xét tam giác $MQB$ và $MBD$ có:
$\widehat{M}$ chung
$\widehat{MBQ}=\widehat{MDB}$ (góc tạo bởi tiếp tuyến và dây cung bằng góc nội tiếp chắn cung đó)
$\Rightarrow \triangle MQB\sim \triangle MBD$ (g.g)
$\Rightarrow \frac{MQ}{MB}=\frac{MB}{MD}$
$\Rightarrow MQ.MD=MB^2(2)$
Từ $(1); (2)\Rightarrow MQ.MD=MC.MO$