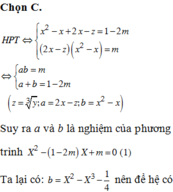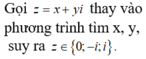Tìm nghiệm của phương trình sau: ( x - z )( x2 + xz + z2 ) = xy3 + 3z3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
13 tháng 6 2018
Chọn đáp án A
*Với z=0 thì phương trình đã cho trở thành 1=0 (Vô lý).
*Với z ≠ 0 ta chia cả hai vế của phương trình cho z 2 và được
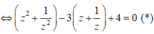
Phương trình (*) trở thành
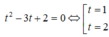
Vậy T = z 1 + z 2 + z 3 = 3
HA
0
1 tháng 11 2021
\(1,\\ a,=\left(x-y\right)^2-z^2=\left(x-y-z\right)\left(x-y+z\right)\\ b,=a^2\left(a-x\right)-y\left(a-x\right)=\left(a^2-y\right)\left(a-x\right)\\ c,=\left(x-y\right)^2-z\left(x-y\right)=\left(x-y\right)\left(x-y-z\right)\\ d,=x\left(x-2y\right)+t\left(x-2y\right)=\left(x+t\right)\left(x-2y\right)\\ 2,\\ \Rightarrow x^2-4x+4-x^2+9=6\\ \Rightarrow-4x=-7\Rightarrow x=\dfrac{7}{4}\\ 3,\\ a,x^2+2x+2=\left(x+1\right)^2+1\ge1>0\\ b,-x^2+4x-5=-\left(x-2\right)^2-1\le-1< 0\)
CM
22 tháng 4 2019
Chọn D
Gọi z=x+yi thay vào phương trình tìm x, y, suy ra zÎ{0;-i;i}