cho phương trình x4 -2mx2+m2-4=0
Tìm m để phương trình có bốn nghiệm phân biệt
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
N
2
28 tháng 3 2021
Đặt \(x^2=a\left(a\ge0\right)\)
Phương trình trở thành \(a^2-5a+m=0\)
\(\Delta=\left(-5\right)^2-4\cdot1\cdot m=-4m+25\)
Để phương trình \(x^4-5x^2+m=0\) có đúng 2 nghiệm phân biệt thì phương trình \(a^2-5a+m=0\)(\(a=x^2\)) có nghiệm kép
\(\Leftrightarrow\Delta=0\)
\(\Leftrightarrow-4m+25=0\)
\(\Leftrightarrow-4m=-25\)
hay \(m=\dfrac{25}{4}\)
Vậy: \(m=\dfrac{25}{4}\)
NV
Nguyễn Việt Lâm
Giáo viên
28 tháng 3 2021
Đặt \(t=x^2\ge0\Rightarrow t^2-5t+m=0\) (1)
Ứng với mỗi giá trị \(t>0\) luôn cho 2 giá trị x phân biệt tương ứng nên pt đã cho có 2 nghiệm pb khi và chỉ khi (1) có đúng 1 nghiệm dương và 1 nghiệm âm
\(\Leftrightarrow\) (1) có 2 nghiệm trái dấu
\(\Leftrightarrow ac=m< 0\)
Vậy \(m< 0\)
31 tháng 3 2023
x1+x2=2m+2; x1x2=m^2+4
x1^2+2(m+1)x2<=2m^2+20
=>x1^2+x2(x1+x2)<=2m^2+20
=>x1^2+x2x1+x2^2<=2m^2+20
=>(x1+x2)^2-x1x2<=2m^2+20
=>(2m+2)^2-(m^2+4)<=2m^2+20
=>4m^2+8m+4-m^2-4-2m^2-20<=0
=>m^2-8m-20<=0
=>m<=-10 hoặc m>2
LD
31 tháng 3 2023
\(x^2-2\left(m+1\right)x+m^2+4=0\left(1\right)\)
Để phương trình có hai nghiệm phân biệt thì \(\Delta'>0\) hay \(\Delta'=\left(m+1\right)^2-m^2-4=m^2+2m+1-m^2-4=2m-4>0\Leftrightarrow m>2\)
Theo hệ thức Viét ta có : \(\left\{{}\begin{matrix}x_1+x_2=2\left(m+1\right)\\x_1.x_2=m^2+4\end{matrix}\right.\)
Vì \(x_1^2\) là nghiệm của phương trình (1) nên ta có : \(x_1^2-2\left(m+1\right)x+m^2+4=0\Leftrightarrow x_1^2=2\left(m+1\right)x_1-m^2-4\)
Ta lại có : \(x_1^2+2\left(m+1\right)x_2\le2m^2+20\)
\(\Leftrightarrow2\left(m+1\right)x_1-m^2-4+2\left(m+1\right)x_2\le2m^2+20\)
\(\Leftrightarrow2\left(m+1\right)\left(x_1+x_2\right)-m^2-4\le2m^2+20\)
\(\Leftrightarrow4\left(m+1\right)^2-m^2\le2m^2+20\)
\(\Leftrightarrow4\left(m^2+2m+1\right)-m^2\le2m^2+20\)
\(\Leftrightarrow m^2+8m-16\le0\)
\(\Leftrightarrow-10\le m\le2\)
Kết hợp điều kiện....
CM
26 tháng 12 2017
Chọn đáp án B
Phương trình tương đương với:
(1)
Đặt t = x 2 - 2 x + m , phương trình (1) đưa được về hệ:
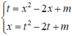
Trừ theo vế của hai phương trình trong hệ trên, ta được:
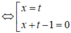
Suy ra
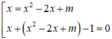
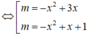
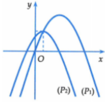
Vẽ trên cùng một hệ trục tọa độ Oxy hai đường parabol P 1 : y = - x 2 + 3 x và P 2 : y = - x 2 + x + 1 (hình vẽ bên).
Xét phương trình hoành độ giao điểm của (P1) và (P2):
Suy ra (P1) cắt (P2) tại điểm 1 2 ; 5 4 .
Để phương trình đã cho có bốn nghiệm phân biệt
Đường thẳng y = m cắt (P1) tại hai điểm và cắt (P2) tại hai điểm.
Quan sát đồ thị ta thấy m ≤ 5 4 .
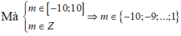
Vậy có 12 giá trị của m thỏa mãn yêu cầu bài toán.
AH
Akai Haruma
Giáo viên
4 tháng 4 2021
Lời giải:
Để pt có 2 nghiệm pb thì $\Delta=25-4(m-2)>0\Leftrightarrow m< \frac{33}{4}$
Áp dụng định lý Viet: $x_1+x_2=5$ và $x_1x_2=m-2$
Khi đó:
$x_1^2+4x_1+x_2=9$
$\Leftrightarrow x_1^2+3x_1+(x_1+x_2)=9$
$\Leftrightarrow x_1^2+3x_1+5=9\Leftrightarrow x_1^2+3x_1-4=0$
$\Leftrightarrow (x_1-1)(x_1+4)=0$
$\Leftrightarrow x_1=1$ hoặc $x_1=-4$
$x_1=1$ thì $x_2=4$
$\Rightarrow m-2=x_1x_2=4\Rightarrow m=6$
$x_1=-4$ thì $x_2=9$
$\Rightarrow m-2=x_1x_2=-36\Rightarrow m=-34$
Vì $m< \frac{33}{4}$ nên cả 2 giá trị này đều thỏa
16 tháng 4 2022
\(\text{Δ}=\left(2m+2\right)^2-4\left(m+3\right)\)
\(=4m^2+8m+4-4m-12\)
\(=4m^2+4m-8\)
\(=4\left(m+2\right)\left(m-1\right)\)
Để phương trình có hai nghiệm phân biệt thì (m+2)(m-1)>0
=>m>1 hoặc m<-2
Theo đề, ta có: 2(m+1)>2
=>m+1>1
hay m>0
=>m>1
bài này đặt x^2=t(t>=0) rùi giải pt bậc 2 tìm 2 nghiệm phân biệt cùng dương là ra