giải các phương trình sau bằng công thức nghiệm hoặc công thức no thu gọn:
d)\(9x^2+30x+25=0\)
e)\(x^2-4\sqrt{5}x+4=0\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
27 tháng 2 2022
BÀI 1. Giải các phương trình sau bằng công thức nghiệm hoặc (công thức nghiện thu gọn).
1) x2 - 11x + 38 = 0 ;
2) 6x2 + 71x + 175 = 0 ;
3) 5x2 - 6x + 27 =0 ;
4) - 30x2 + 30x - 7,5 = 0 ;
5) 4x2 - 16x + 17 = 0 ;
6) x2 + 4x - 12 = 0 ;
25 tháng 2 2022
b; \(\text{Δ}=1^2-4\cdot\left(-2\right)\cdot\left(-3\right)=1-4\cdot6=-23< 0\)
Do đó: Phương trình vô nghiệm
c: \(\text{Δ}=1^2-4\cdot\left(-1\right)\cdot11=1+44=45>0\)
Do đó: Phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{1-3\sqrt{5}}{-2}=\dfrac{3\sqrt{5}-1}{2}\\x_2=\dfrac{-3\sqrt{5}-1}{2}\end{matrix}\right.\)
25 tháng 2 2022
a, \(\Delta'=2-\left(-6\right)=8>0\)
vậy pt luôn có 2 nghiệm pb
\(x_1=-\sqrt{2}-2\sqrt{2};x_2=-\sqrt{2}+2\sqrt{2}\)
b, \(\Delta=1-4\left(-3\right)\left(-2\right)=1-16< 0\)
pt vô nghiệm
c, \(\Delta=1-4.11\left(-1\right)=1+44=45>0\)
pt luôn có 2 nghiệm pb
\(x_1=\dfrac{-1-3\sqrt{5}}{-2};x_2=\dfrac{-1+3\sqrt{5}}{-2}\)
11 tháng 1 2022
a: =>(x-7)(x+3)=0
hay \(x\in\left\{7;-3\right\}\)
b: =>2x+7=0
hay x=-7/2
c: \(\Delta=50-4\cdot6\cdot2=50-48=2\)
Vì Δ>0 nên phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{5\sqrt{2}-\sqrt{2}}{12}=\dfrac{\sqrt{2}}{3}\\x_2=\dfrac{\sqrt{2}}{2}\end{matrix}\right.\)
9 tháng 11 2021
\(1,\Delta=\left(-11\right)^2-4\cdot30=1\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{11-1}{2}=5\\x=\dfrac{11+1}{2}=6\end{matrix}\right.\\ 2,\Delta=\left(-1\right)^2-4\left(-20\right)=81\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1-\sqrt{81}}{2}=-4\\x=\dfrac{1+\sqrt{81}}{2}=5\end{matrix}\right.\\ 3,\Delta=14^2-4\cdot24=100\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{-14-\sqrt{100}}{2}=-12\\x=\dfrac{-14+\sqrt{100}}{2}=-2\end{matrix}\right.\\ 4,\Delta=8^2-4\left(-2\right)3=88\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{-8-\sqrt{88}}{6}=\dfrac{-4+\sqrt{22}}{3}\\x=\dfrac{-8+\sqrt{88}}{6}=\dfrac{-4-\sqrt{22}}{3}\end{matrix}\right.\)
21 tháng 3 2023
a: 3x^2-4x+1=0
a=3; b=-4; c=1
Vì a+b+c=0 nên phương trình có hai nghiệm là:
x1=1 và x2=c/a=1/3
b: -x^2+6x-5=0
=>x^2-6x+5=0
a=1; b=-6; c=5
Vì a+b+c=0 nên phương trình có hai nghiệm là;
x1=1; x2=5/1=5
PT
1
CM
23 tháng 1 2018
Phương trình bậc hai: 
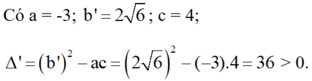
Phương trình có hai nghiệm phân biệt :
27 tháng 2 2020
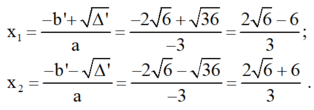
a)
5x2−3x=0⇔x(5x−3)=05x2−3x=0⇔x(5x−3)=0
⇔ x = 0 hoặc 5x – 3 =0
⇔ x = 0 hoặc x=35.x=35. Vậy phương trình có hai nghiệm: x1=0;x2=35x1=0;x2=35
Δ=(−3)2−4.5.0=9>0√Δ=√9=3x1=3+32.5=610=35x2=3−32.5=010=0Δ=(−3)2−4.5.0=9>0Δ=9=3x1=3+32.5=610=35x2=3−32.5=010=0
b)
3√5x2+6x=0⇔3x(√5x+2)=035x2+6x=0⇔3x(5x+2)=0
⇔ x = 0 hoặc √5x+2=05x+2=0
⇔ x = 0 hoặc x=−2√55x=−255
Vậy phương trình có hai nghiệm: x1=0;x2=−2√55x1=0;x2=−255
Δ=62−4.3√5.0=36>0√Δ=√36=6x1=−6+62.3√5=06√5=0x2=−6−62.3√5=−126√5=−2√55Δ=62−4.35.0=36>0Δ=36=6x1=−6+62.35=065=0x2=−6−62.35=−1265=−255
c)
2x2+7x=0⇔x(2x+7)=02x2+7x=0⇔x(2x+7)=0
⇔ x = 0 hoặc 2x + 7 = 0
⇔ x = 0 hoặc x=−72x=−72
Vậy phương trình có hai nghiệm: x1=0;x2=−72x1=0;x2=−72
Δ=72−4.2.0=49>0√Δ=√49=7x1=−7+72.2=04=0x2=−7−72.2=−144=−72Δ=72−4.2.0=49>0Δ=49=7x1=−7+72.2=04=0x2=−7−72.2=−144=−72
d)
2x2−√2x=0⇔x(2x−√2)=02x2−2x=0⇔x(2x−2)=0
⇔ x = 0 hoặc 2x−√2=02x−2=0
⇔ x = 0 hoặc x=√22x=22
Δ=(−√2)2−4.2.0=2>0√Δ=√2x1=√2+√22.2=2√24=√22x2=√2−√22.2=04=0
d, \(\Delta'=225-25.9=0\)pt có nghiệm kép
\(x_1=x_2=\dfrac{-15}{9}=-\dfrac{5}{3}\)
e, \(\Delta'=4.5-4=16>0\)pt có 2 nghiệm pb
\(x_1=2\sqrt{5}-4;x_2=2\sqrt{5}+4\)
d: \(\Leftrightarrow\left(3x+5\right)^2=0\)
=>3x+5=0
hay x=-5/3
e: \(\text{Δ}=\left(4\sqrt{5}\right)^2-4\cdot1\cdot4=80-16=64>0\)
Do đó: Phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{4\sqrt{5}-8}{2}=2\sqrt{5}-4\\x_2=2\sqrt{5}+4\end{matrix}\right.\)