x14 + x24 =
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
Theo định lý Viet:
$x_1+x_2=3$
$x_1x_2=-7$
Khi đó:
$A=\frac{1}{x_1-1}+\frac{1}{x_2-1}=\frac{x_2-1+x_1-1}{(x_1-1)(x_2-1)}$
$=\frac{(x_1+x_2)-2}{x_1x_2-(x_1+x_2)+1}=\frac{3-2}{-7-3+1}=\frac{-1}{9}$
$E=x_1^4+x_2^4=(x_1^2+x_2)^2-2(x_1x_2)^2=[(x_1+x_2)^2-2x_1x_2]^2-2(x_1x_2)^2$
$=[3^2-2(-7)]^2-2(-7)^2=431$


x 1 4 − x 2 4 = x 1 2 + x 2 2 x 1 2 − x 2 2 = x 1 + x 2 2 − 2 x 1 x 2 x 1 − x 2 x 1 + x 2
Mà x 1 − x 2 = ( x 1 − x 2 ) 2 = ( x 1 + x 2 ) 2 − 4 x 1 x 2
= ( 2 m + 2 ) 2 − 4 ( m 2 + 2 ) = 8 m − 4
Suy ra x 1 4 − x 2 4 = ( 2 m + 2 ) 2 − 2 ( m 2 + 2 ) 8 m − 4 2 m + 2
= ( 2 m 2 + 8 ) 8 m − 4 2 m + 2
Suy ra x 1 4 − x 2 4 = 16 m 2 + 64 m
⇔ ( 2 m 2 + 8 m ) 8 m − 4 2 m + 2 = 16 m 2 + 64 m
⇔ ( m 2 + 4 m ) ( 8 m − 4 2 m + 2 − 8 = 0 ⇔ m 2 + 4 m = 0 ( 1 ) 8 m − 4 2 m + 2 = 8 ( 2 )
Ta có (1) ⇔ m = 0 m = − 4 (loại)
![]()
⇔ m = 1 (thỏa mãn (*)
Vậy m = 1 thỏa mãn yêu cầu bài toán.
Đáp án cần chọn là: C

Để pt có nghiệm \(\Leftrightarrow\Delta\ge0\Leftrightarrow4-4\left(m-1\right)\ge0\)\(\Leftrightarrow2\ge m\)
Theo viet: \(\left\{{}\begin{matrix}x_1+x_2=2\left(1\right)\\x_1x_2=m-1\end{matrix}\right.\)
\(x_1^4-x_1^3=x_2^4-x_2^3\)
\(\Leftrightarrow\left(x_1^4-x_2^4\right)-\left(x_1^3-x_2^3\right)=0\)
\(\Leftrightarrow\left(x_1-x_2\right)\left(x_1+x_2\right)\left(x_1^2+x_2^2\right)-\left(x_1-x_2\right)\left(x_1^2+x_1x_2+x_2^2\right)=0\)
\(\Leftrightarrow\left(x_1-x_2\right)\left[2\left(x_1^2+x_2^2\right)-x_1^2-x_1x_2-x_2^2\right]=0\)
\(\Leftrightarrow\left(x_1-x_2\right)\left(x_1^2+x_2^2-x_1x_2\right)=0\)
\(\Leftrightarrow x_1-x_2=0\) (2) ( vì \(x_1^2-x_1x_2+x_2^2>0;\forall x,y\))
Từ (1) (2) \(\Rightarrow x_1=x_2=1\)
\(\Rightarrow x_1x_2=m-1=1\) \(\Leftrightarrow m=2\) (Thỏa)
Vậy...

a: Khi m=4 thì phương trình trở thành \(x^2-4x+3=0\)
=>(x-3)*(x-1)=0
=>x=3 hoặc x=1
b: \(x_1+x_2=m\)
\(x_1x_2=m-1\)
\(x_1^2+x_2^2=\left(x_1+x_2\right)^2-2x_1x_2=m^2-2\left(m-1\right)=m^2-2m+2\)
\(x_1^4+x_2^4=\left(x_1^2+x_2^2\right)^2-2\left(x_1x_2\right)^2\)
\(=\left(m^2-2m+2\right)^2-2\cdot\left(m-1\right)^2\)
\(=m^4+4m^2+4-4m^3+4m^2-8m-2m^2+4m-2\)
\(=m^4-4m^3+2m^2-4m+2\)

Đáp án A
Phương trình hoành độ giao điểm của (C) và Ox là x 4 − m x 2 + m = 0 * .
Đặt t = x 2 ≥ 0 khi đó * ⇔ f t = t 2 − m t + m = 0
Để (*) có 4 nghiệm phân biệt ⇔ f t = 0 có 2 nghiệm dương phân biệt t 1 , t 2
Khi đó, gọi t 1 , t 2 t 1 < t 2 là hai nghiệm phân biệt của f t = 0
Suy ra:
x 1 = − t 2 ; x 2 = − t 1 ; x 3 = t 1 ; x 4 = t 2 ⇒ x 1 4 + x 2 4 + x 3 4 + x 4 4 = 2 t 1 2 + t 2 2 = 30
Mà t 1 + t 2 = m t 1 t 2 = m
⇒ t 1 2 + t 2 2 = t 1 + t 2 2 − 2 t 1 t 2 = m 2 − 2 m
suy ra m > 4 m 2 − 2 m = 15 ⇔ m = 5.

Ta có:
(A): x14 : x = x14 - 1 = x13
(B): x7 .x2 = x7+2 = x9
(C): x8. x6 = x8+6 = x14
(D): x14.x = x14+1 = x15
Chọn (C)x8. x6.

\(\Leftrightarrow7x=-51\cdot14-13=-727\)
hay x=-727/7

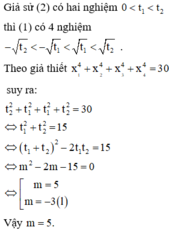

x14 + x24 = (x12 + x22)2
HT
\(x_1^4+x_2^4=\left(x_1^2+x_2^2\right)^2-2x_1^2x_2^2\)
\(=\left[\left(x_1+x_2\right)^2-2x_1x_2\right]^2-2x_1^2x_2^2\)