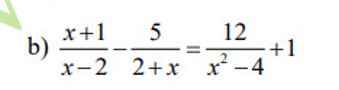
helpppppppppppppppp! Bài này cần ĐKXĐ ko ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 2: Chọn C
Bài 4:
a: \(\widehat{C}=180^0-80^0-50^0=50^0\)
Xét ΔABC có \(\widehat{A}=\widehat{C}< \widehat{B}\)
nên BC=AB<AC
b: Xét ΔABC có AB<BC<AC
nên \(\widehat{C}< \widehat{A}< \widehat{B}\)

a: Xét tứ giác BFCE có
D là trung điểm của BC
D là trung điểm của FE
Do dó: BFCE là hình bình hành
b: Xét tứ giác ABFE có
AB//FE
AB=FE
Do đó: ABFE là hình bình hành
mà \(\widehat{FAB}=90^0\)
nên ABFE là hình chữ nhật

\(a,\dfrac{4}{5}\times\dfrac{7}{3}\times\dfrac{3}{4}=\dfrac{4\times7\times3}{5\times3\times4}=\dfrac{7}{5}\)
\(b,\left(\dfrac{1}{2}+\dfrac{1}{3}\right)\times\dfrac{1}{4}\)
\(=\left(\dfrac{3}{6}+\dfrac{2}{6}\right)\times\dfrac{1}{4}\)
\(=\dfrac{5}{6}\times\dfrac{1}{4}\)
\(=\dfrac{5}{24}\)
\(c,\left(\dfrac{2}{3}+\dfrac{2}{5}\right)\times\dfrac{2}{7}\)
\(=\left(\dfrac{10}{35}+\dfrac{6}{35}\right)\times\dfrac{2}{7}\)
\(=\dfrac{16}{15}\times\dfrac{2}{7}\)
\(=\dfrac{32}{105}\)
Cách `1`
`a)4/5 xx 7/3 xx 3/4`
`=28/15 xx 3/4`
`=84/60`
`=7/5`
__
`b)(1/2+1/3)xx1/4`
`=(3/6+2/6)xx1/4`
`=5/6xx1/4`
`=5/24`
__
`c)(2/3+2/5)xx2/7`
`=(10/15+6/15)xx2/7`
`=16/15xx2/7`
`=32/105`
___________________________
Cách `2`:
`a)4/5 xx 7/3 xx 3/4`
`=4/5 xx (7/3 xx 3/4)`
`=4/5 xx 7/4`
`=7/5`
__
`b)(1/2+1/3)xx1/4`
`=1/2 xx 1/4 + 1/3 xx 1/4`
`= 1/8 + 1/12`
`= 3/24+2/24`
`=5/24`
__
`c)(2/3+2/5)xx2/7`
`=2/3 xx 2/7 + 2/5 xx 2/7`
`=4/21 + 4/35`
`= 20/105+12/105`
`=32/105`
`#QiN`

1 I have sat X here for 30 minutes.
=> Tôi đã ngồi ở đây được 30 phút rồi.
2 She has stood X alone since the morning.
=> Cô ấy đã đứng một mình từ sáng đến giờ
3 They have lain X on my bed for an hour
=> Họ đã nằm trên giường của tôi được một tiếng rồi
4 We had gone X to school by 6:30 this morning.
=> Chúng tôi đã đến trường trước 6:30 sáng nay
5 This man had run X 2 kilometers by this time yesterday
=> Người đàn ông này đã chạy được 2 cây số vào thời điểm này hôm qua
6 The girl had come X to the party by 7:45 pm yesterday
=> Cô gái đó đã đến bữa tiệc trước 7:45 tối hôm qua
7 The people will have driven X to the center for some minutes by this time tomorrow
=> Mọi người sẽ đã lái xe đến trung tâm trong vài phút vào thời điểm này ngày mai
8 He will have flown planes as a pilot for 20 years by 2020
=> Anh ấy sẽ đã lái máy bay với tư cách phi công trong 20 năm tính đến năm 2020
9 The children have swum X since then
=> Những đứa trẻ đã bơi từ đó đến giờ
10 I haven’t eaten meat (or anything) for some years
=> Tôi đã không ăn thịt trong vài năm rồi

Bài 1
Mình làm mẫu một số câu thôi nhé
\(9,\sqrt{5}=\left(\sqrt{5}\right)^2=5\\ \sqrt{6}=\left(\sqrt{6}\right)^2=6\)
Vì \(5< 6\)
\(\Rightarrow\sqrt{5}< \sqrt{6}\)
\(10,2\sqrt{5}=\left(2\sqrt{5}\right)^2=20\\ \sqrt{7}=\left(\sqrt{7}\right)^2=7\)
Vì \(20>7\)
\(\Rightarrow2\sqrt{5}>\sqrt{7}\)
\(11,5\sqrt{2}=\left(5\sqrt{2}\right)^2=50\\ 2\sqrt{3}=\left(2\sqrt{3}\right)^2=12\)
Vì \(50>12\Rightarrow5\sqrt{2}>2\sqrt{3}\)
\(12,2\sqrt{6}=\left(2\sqrt{6}\right)^2=24\\ 5=5^2=25\)
Vì \(25>24\Rightarrow5>2\sqrt{6}\)
\(13,\sqrt{7}=\left(\sqrt{7}\right)^2=7\\ 2=2^2=4\)
Vì \(7>4\Rightarrow\sqrt{7}>2\)
\(14,3=3^2=9\\ \sqrt{5}=\left(\sqrt{5}\right)^2=5\)
Vì \(9>5\Rightarrow3>\sqrt{5}\)
\(15,3\sqrt{6}=\left(3\sqrt{6}\right)^2=54\)
Vì \(54>1\Rightarrow3\sqrt{6}>1\)
\(16,2\sqrt{2}=\left(2\sqrt{2}\right)^2=8\\ 3=3^2=9\)
Vì \(8< 9\Rightarrow2\sqrt{2}< 3\)
Phương pháp làm dạng bài này là bình phương hai vế rồi so sánh
Bài 2
Gợi ý : Biểu thức dưới dấu căn \(\ge\) 0
Lưu ý : Nếu biểu thức dưới dấu căn ở dưới mẫu thì \(>0\)
\(21,ĐK:4x^2-12x+9>0\\ \Rightarrow\left(2x-3\right)^2>0\\ \Leftrightarrow x\ne\dfrac{3}{2}\)
\(22,ĐK:x^2-8x+15\ge0\\ \Rightarrow\left[{}\begin{matrix}x\le3\\x\ge5\end{matrix}\right.\)
\(23,ĐK:\left\{{}\begin{matrix}x-2\ge0\\x-5\ne0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x\ge2\\x\ne5\end{matrix}\right.\)
\(24,ĐK:\left\{{}\begin{matrix}\dfrac{2+x}{5-x}\ge0\\5-x\ne0\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}2+x\ge0\\5-x\ge0\\x\ne5\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}x\ge-2\\x\le5\\x\ne5\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}x\ge-2\\x< 5\end{matrix}\right.\left(t/m\right)\)
Hoặc
\(\left\{{}\begin{matrix}2+x\le0\\5-x\le0\\5-x\ne0\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}x\le-2\\x\ge5\\x\ne5\end{matrix}\right.\left(loại\right)\)

ĐKXĐ:\(x\ne\pm2\)
\(\dfrac{x+1}{x-2}-\dfrac{5}{2+x}=\dfrac{12}{x^2-4}+1\\ \Leftrightarrow\dfrac{\left(x+1\right)\left(x+2\right)}{\left(x+2\right)\left(x-2\right)}-\dfrac{5\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}-\dfrac{12}{\left(x-2\right)\left(x+2\right)}-\dfrac{\left(x-2\right)\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}=0\\ \Leftrightarrow\dfrac{x^2+3x+2-5x+10-12-x^2+4}{\left(x-2\right)\left(x+2\right)}=0\)
\(\Rightarrow-2x+4=0\\ \Leftrightarrow x=2\left(ktm\right)\)
\(\Rightarrow x^2+3x+2-5x+10=12+x^2-4\)
\(\Leftrightarrow-2x+12=8\Leftrightarrow x=2\left(ktm\right)\)
pt vô nghiệm