Có 3 đường ống trong một bể bơi. Ống A và ống B dùng để đưa nước vào còn ống C dùng để thoát nước khỏi bể. Lúc đầu ống A được mở để bơm nước vào bể. Khi đó, ống C vô tình được mở. Bộ phận sửa chữa mất 8 tiếng để phát hiện ra điều trên và lúc này bể đã đầy 2/3. Đội sửa chữa ngay lập tức đóng ống C và mở ống B để đưa nước vào. Sau 2 tiếng, bể cuối cùng đã đầy. Bộ phận sửa chữa cũng phát hiện ra rằng trong suốt quá trình trên, lượng nước được thoát ra bằng ống C gấp đôi lượng nước đưa vào bằng ống B. Hỏi ống C mất bao lâu để thoát hết nước trong một bể đầy?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án: A
Cột nước còn đọng lại được trong ống mao dẫn là do tác dụng cân bằng giữa trọng lượng P của cột nước với tổng các lực dính ướt fc của thành ống tạo thành mặt khum lõm ở đầu trên và mặt khum lồi ở đầu dưới của cột nước (hình vẽ).
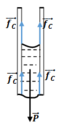
Tại vị trí tiếp xúc giữa hai mặt khum của cột nước với thành ống, các lực dính ướt fc đều hướng thẳng đứng lên phía trên và có cùng độ lớn với lực căng bề mặt Fc của nước.
Fd = Fc = σ.π.d
với d là đường kính của ống mao dẫn và σ là hệ số căng bề mặt của nước.
Trọng lượng của cột nước:
P = mg = ρghπd2/4
Khi đó điều kiện cân bằng của cột nước đọng lại trong ống là:
P = 2Fd
⇒ ρ.g.h.π.d2/4 = 2σ.π.d
Từ đó suy ra:
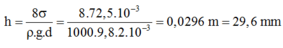

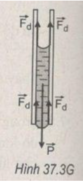
Cột nước còn đọng lại được trong ống mao dẫn là do tác dụng cân bằng giữa trọng lượng P của cột nước với tổng các lực dính ướt F d của thành ống tạo thành mặt khum lõm ở đầu trên và mặt khum lồi ở đầu dưới của cột nước (H.37.3G). Tại vị trí tiếp xúc giữa hai mặt khum của cột nước với thành ống, các lực dính ướt F d đều hướng thẳng đứng lên phía trên và có cùng độ lớn với lực căng bề mặt F c của nước.
F d = F c = σ π d
với d là đường kính của ống mao dẫn và σ là hệ số căng bề mặt của nước. Nếu gọi D là khối lượng riêng của nước và h là độ cao của cột nước trong ống thì trọng lượng cột nước bằng :
P = mg = Dgh π d 2 /4
Khi đó điều kiện cân bằng của cột nước đọng lại trong ống là :
P = 2 F d ⇒ Dgh d 2 /4 = 2 σ π d
Từ đó suy ra :
![]()

Sau 4 phút hai bể bơm được số phần bể là :
\(4\times\left(\frac{1}{15}+\frac{1}{20}\right)=\frac{7}{15}\text{ bể}\)
thể tích còn lại của bể là : \(1-\frac{7}{15}=\frac{8}{15}\text{ bể}\)
Ống B cần số phút để làm đầy bể là : \(\frac{8}{15}:\frac{1}{20}=\frac{32}{3}\text{ phút}\)
Vậy tổn số thời gian làm đầy bể là : \(4+\frac{32}{3}=\frac{44}{3}\text{ phút}\)

Mỗi phút vòi thứ nhất bơm đuuợc \(\frac{1}{20}\text{ bể}\) vòi thứ hai bơm được \(\frac{1}{15}\text{ bể}\)
vậy trong 1 phút hai vòi bơm được thể tích bể là : \(\frac{1}{20}+\frac{1}{15}=\frac{7}{60}\text{ bể}\)
vậy nếu mở cả hai vòi thì mất \(\frac{60}{7}\text{ phút }\) để bơm đầy bể
Gọi năng suất làm việc của ống B trong 1 giờ là x (bể) Đk : x<1
năng suất làm việc của ống C trong 1 giờ là 2x(bể)
năng suất làm việc của ống A trong 1 giờ là 1/12+2x(bể)
Theo đề bài , ta có phương trình:
2(1/12+2x+x)=1/3 <=>(1/12+3x)=1/6 <=>3x=1/12 <=>x=1/36
Năng suất làm việc của ống C trong 1 giờ là: 2*1/36=1/18(bể)
Thời gian để ống C thoát hết 1 bể nước đầy là :1/(1/18)=18(giờ)
Vậy thời gian để ống C thoát hết 1 bể nước đầy là 18 giờ
toán hại não qá éo bít t new học lớp 5