GIÚP EM CÂU B VỚI ẠA
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
2 tháng 3 2022
1: Thay x=16 vào A, ta được:
\(A=\dfrac{4-1}{4+3}=\dfrac{3}{7}\)
2: \(P=A:B\)
\(=\dfrac{\sqrt{x}-1}{\sqrt{x}+3}:\dfrac{x-3\sqrt{x}-x-6\sqrt{x}-9+x+11\sqrt{x}+6}{x-9}\)
\(=\dfrac{\sqrt{x}-1}{1}\cdot\dfrac{\sqrt{x}-3}{x+2\sqrt{x}-3}=\dfrac{\sqrt{x}-3}{\sqrt{x}+3}\)
4 tháng 6 2023
b: kẻ đường kính AD
góc ACD=90 độ=góc ABD
=>AC vuông góc CD và AB vuông góc BD
=>BH//CD và CH//BD
=>BDCH là hbh
=>H,N,D thẳng hàng và N là trung điểm của HD
=>NT là đường trung bình của ΔAHD
=>NT//AD và NT=1/2AD=OA
=>NT//OA
=>ATNO là hbh
EN=1/2BC
=>EN=BN
=>ΔNEB cân tại N
=>góc NBE=góc NEB
EJ=1/2AH=JH
=>ΔJEH cân tại J
=>góc JEH=góc JHE
góc NBE+Góc ACB=90 độ
góc HAC+góc ACB=90 độ
=>góc NBE=góc HAC
mà góc JHE+góc HAC=90 độ
nên góc JHE+góc NBE=90 độ
=>góc JEN=90 độ
26 tháng 1 2022
a: Khi m=-2 thì (d): y=-5x-2
ii: Tọa độ giao điểm của (P) và (d) là:
\(\left\{{}\begin{matrix}2x^2+5x+2=0\\y=2x^2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\in\left\{-\dfrac{1}{2};-2\right\}\\y\in\left\{\dfrac{1}{2};8\right\}\end{matrix}\right.\)
Vậy: M(-1/2;1/2); N(-2;8)
\(OM=\sqrt{\left(-\dfrac{1}{2}-0\right)^2+\left(\dfrac{1}{2}-0\right)^2}=\sqrt{\dfrac{1}{4}+\dfrac{1}{4}}=\dfrac{\sqrt{2}}{2}\)
\(ON=\sqrt{\left(-2-0\right)^2+\left(8-0\right)^2}=2\sqrt{17}\)
\(MN=\sqrt{\left(-2+\dfrac{1}{2}\right)^2+\left(8-\dfrac{1}{2}\right)^2}=\sqrt{\dfrac{9}{4}+\dfrac{225}{4}}=\dfrac{3\sqrt{26}}{2}\)
\(P=OM+ON+NM\simeq4,93\left(cm\right)\)
\(S=\sqrt{4,93\cdot\left(4,93-\dfrac{\sqrt{2}}{2}\right)\cdot\left(4.93-2\sqrt{17}\right)\left(4.93-\dfrac{3\sqrt{26}}{2}\right)}=13,7\left(cm^2\right)\)
LN
mn giúp em câu này với ạa
0
AM
28 tháng 1 2022
Với m=-2
Phương trình tọa độ giao điểm của (d) và (P) là:
\(2x^2=\left(-2-3\right)x+\left(-2\right)\Leftrightarrow2x^2+5x+2=0\Leftrightarrow\)\(\left[{}\begin{matrix}x=-\dfrac{1}{2}\\x=-2\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}y=\dfrac{1}{2}\\y=8\end{matrix}\right.\)
Gọi \(M\left(-\dfrac{1}{2};\dfrac{1}{2}\right),N\left(-2;8\right)\) và kẻ \(NH\perp MO\) ta có hình vẽ như sau:
Gọi phương trình đường thẳng MO là: ax+b=y
\(\left\{{}\begin{matrix}a.0+b=0\\-2a+b=8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=0\\a=-4\end{matrix}\right.\)
Phương trình đường thẳng MO là: -4x=y
Gọi phương trình đường thẳng NH là: ax+b=y
Để NH vuông góc với MO thì: a.a'=-1 \(\Leftrightarrow a.\left(-4\right)=-1\Leftrightarrow a=\dfrac{1}{4}\)
Ta có: \(y=\dfrac{1}{4}x+b\Leftrightarrow\dfrac{1}{2}=\dfrac{1}{4}.\dfrac{-1}{2}+b\Rightarrow b=\dfrac{5}{8}\)
Phương trình đường thẳng NH là: \(y=\dfrac{1}{4}x+\dfrac{5}{8}\)
Phương trình tọa độ giao điểm của NH và MO là: \(-4x=\dfrac{1}{4}x+\dfrac{5}{8}\Leftrightarrow x=\dfrac{-5}{34}\Rightarrow y=\dfrac{10}{17}\)
Độ dài đoạn NH là: NH= \(\sqrt{\left(-\dfrac{5}{34}--\dfrac{1}{2}\right)^2+\left(\dfrac{10}{17}-\dfrac{1}{2}\right)^2}=\dfrac{3\sqrt{17}}{34}\)
Độ dài đoạn MO là: MO=\(\sqrt{\left(-2-0\right)^2+\left(8-0\right)^2}=2\sqrt{17}\)
Diện tích tam giác OMN là: \(S=\dfrac{1}{2}NH.OM=\dfrac{1}{2}.\dfrac{3\sqrt{17}}{34}.2\sqrt{17}\)=1,5(đvdt)
NB
1
27 tháng 12 2023
Câu 2.
Nhiệt lượng bếp tỏa ra trong thời gian \(t=3min=180s\) là:
\(Q=UIt=RI^2t=60\cdot2,5^2\cdot180=675000J\)
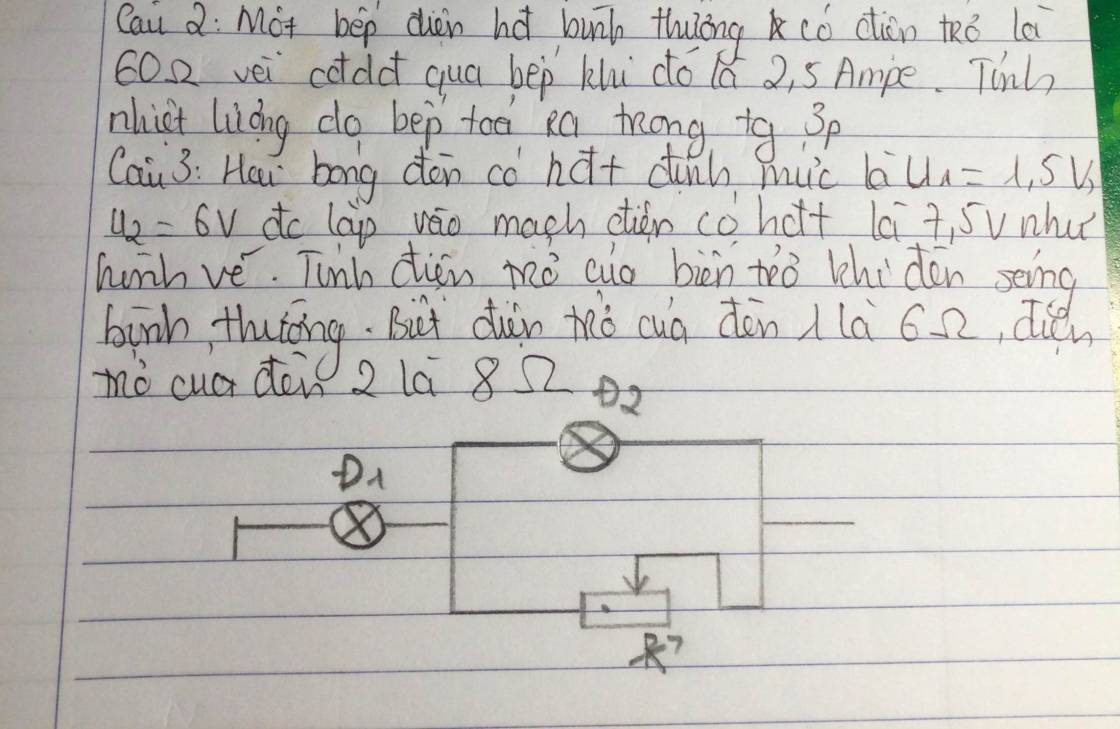
Câu 3.
\(I_{Đ1}=\dfrac{U_{Đ1}}{R_{Đ1}}=\dfrac{6}{6}=1A\)
\(I_{Đ2}=\dfrac{U_{Đ2}}{R_{Đ2}}=\dfrac{1,5}{8}=\dfrac{3}{16}A\)
\(I_b=I_{Đ1}-I_{Đ2}=1-\dfrac{3}{16}=\dfrac{13}{16}A\)
\(R_b=\dfrac{U_b}{I_b}=\dfrac{1,5}{\dfrac{13}{16}}=\dfrac{24}{13}\Omega\)
20 tháng 1 2022
Lá cây xào xạc rơi từ trên cao xuống
--> Mở rộng thành phần Vị Ngữ
PL
giúp em với ạa, bài này là bài tập không phải thi đâu ạa
0
9 tháng 5 2022
\(P=\dfrac{8a+15}{4a+1}=\dfrac{4a+4a+1+1+13}{4a+1}=\dfrac{4a+1}{4a+1}+\dfrac{4a+1}{4a+1}+\dfrac{13}{4a+1}=1+1+\dfrac{13}{4a+1}\)
Để P nguyên thì \(\dfrac{13}{4a+1}\in Z\) hay \(4a+1\in U\left\{13\right\}=\left\{\pm1;\pm13\right\}\)
- 4a+1=1 --> a=0
- 4a+1 = -1 --> a= -1/2 ( loại )
- 4a+1 = 13 --> a=3
-4a+1 = -13 --> a= -7/2 ( loại )
Vậy \(a\in Z=\left\{0;3;\right\}\) thì P nhận giá trị nguyên