cho hình chóp S.ABCD có đáy là hình chữ nhật, SA=AB=a, AD=2a, SA ⊥ (ABCD). gọi E là trung điểm AB. tính khoảng cách giữa CE và SD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HN
19 tháng 11 2021
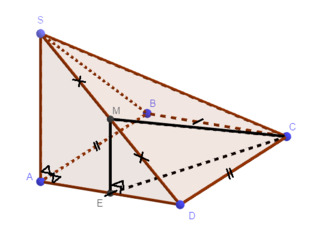
Gọi E là trung điểm AD, ta có: ME//SA (ME là đường trung bình tam giác SAD) và SA, CE chéo nhau; suy ra (MCE) vuông góc (ABCD) và không chứa SA; suy ra SA//(MCE). Suy ra, d(SA,CM) = d(SA,(MCE)) = d(A,(MCE)) = d(D,(MCE)) = d(D,EC) = ED.DC/EC = a.3a/a\(\sqrt{10}\) = 3a\(\sqrt{10}\)/10.
HN
19 tháng 11 2021
Xin lỗi, mình sửa lại bài giải.
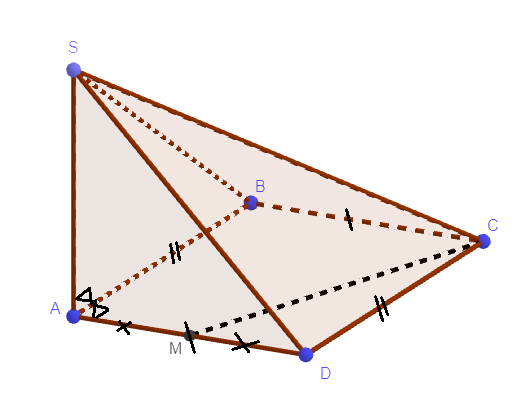
d(SA,CM) = d(A,CM) = d(D,CM) = MD.DC/CM = a.3a/a\(\sqrt{10}\) = 3a\(\sqrt{10}\)/10.
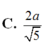
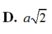
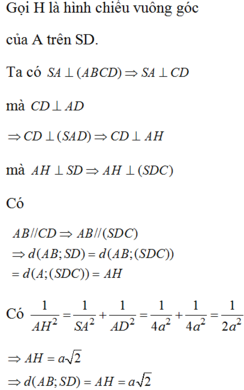
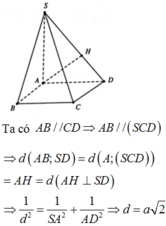
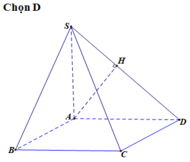
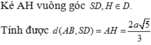
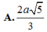
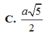
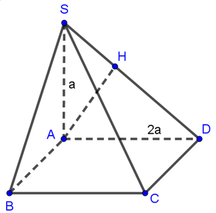
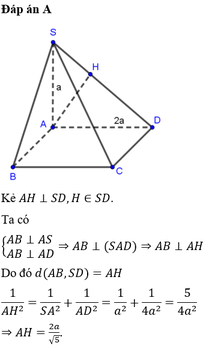
bẹn tk thay chữ vô thoy là đc:
Gọi
là trung điểm của 
. Gọi 
là giao điểm của 
và 
nên 
.
.
, mặt khác 
.
. 
.
.
là hình chữ nhật, 
.
.
,
.
.
Ta kẻ
Ta kẻ
Ta có
Ta có
Ta có
Vậy