cho đường tròn tâm O đường kính AB=2R.Gọi C là trung điểm OA,qua C kẻ dây MN vuông góc với OA tại C.Gọi K là điểm tùy ý trên cung nhỏ BM,H là giao điểm của AK và MN
1)chứng minh 4 điểm B,C,H,K cùng thuộc một đường tròn
2)chứng minh AK.AH=R2
3)Gọi Q,L lần lượt là giao điểm của KA,K với MB.Chứng minh:QL.MB=MQ.LB
GIÚP HỘ MÌNH VỚI CHIỀU MAI MÌNH HỘP RỒI!!!


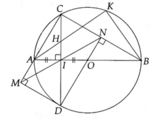
1) Xét (O) có
ΔKAB nội tiếp đường tròn(K,A,B\(\in\)(O))
AB là đường kính
Do đó: ΔKAB vuông tại K(Định lí)
\(\Leftrightarrow\widehat{AKB}=90^0\)
hay \(\widehat{HKB}=90^0\)
Xét tứ giác BKHC có
\(\widehat{HKB}\) và \(\widehat{HCB}\) là hai góc đối
\(\widehat{HKB}+\widehat{HCB}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: BKHC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
hay B,K,H,C cùng thuộc một đường tròn(đpcm)