có bao nhiêu hình tam giác, to hay nhỏ đều được ...
Đọc tiếp
có bao nhiêu hình tam giác, to hay nhỏ đều được
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
10 tháng 10 2019
Đáp án C
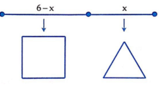
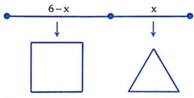
Cắt sợi dây 6 mét đã cho thành hai phần có độ dài lần luột là x mét và 6-x mét 0 < x < 6 . Phần thứ nhất có độ dài x mét được uốn thành hình tam giác đều cạnh bằng x 3 mét. Phần thứ hai có độ dài 6-x mét được uốn thành hình vuông cạnh bằng 6 − x 4 mét.
Diện tích phần I là S 1 = x 3 2 . 3 4 = x 2 3 36 m 2 .
Diện tích phần II là S 2 = 6 − x 4 2 m 2 .
Tổng diện tích hai phần là S x = S 1 + S 2 = x 2 3 36 + 6 − x 4 2 m 2 với x ∈ 0 ; 6
Đạo hàm S ' x = x 3 18 − 6 − x 8 ; S ' x = 0 ⇔ x = 54 9 + 4 3 ∈ 0 ; 6 . Lập bảng biến thiên của hàm số S x trên khoảng 0 ; 6 , ta thấy min S x = S 54 9 + 4 3 .
Khi đó cạnh của tam giác đều bằng 18 9 + 4 3 m .
CM
10 tháng 12 2017
Chọn đáp án C
Gọi độ dài cạnh của hình vuông là x (m) thì độ dài cạnh tam giác đều là 2x (m).
Chiều dài phần dây được uống thành hình vuông (chính là chu vi hình vuông) là 4x (m); chiều dài phần dây được uốn thành tam giác đều (chính là chu vi hình tam giác đều) là 6x(m) .
Suy ra chiều dài phần dây được uốn thành hình tròn là L - 4 x - 6 x = L - 10 x ( m )
Từ đó ta có x ∈ 0 ; L 10
Gọi r là bán kính của đường tròn thì chu vi đường tròn là
Tổng diện tích của ba hình là
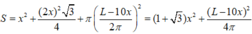
Xét hàm số
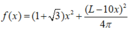
trên 0 ; L 10
Ta có
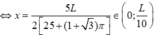
Lập bảng biến thiên ta thấy
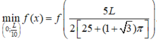
Vậy tổng diện tích của ba hình thu được nhỏ nhất khi x = 5 L 2 25 + 1 + 3 π
suy ra độ dài cạnh của tam giác đều là 2 x = 5 L 25 + 1 + 3 π
NT
chia tam giác thành đều thành các tam giác đều nhỏ hơn ,hỏi có ít nhất là bao nhiêu tam giác đều nhỏ
0
6 tháng 6 2023
a: Số đường chéo là:
\(\dfrac{24\left(24-3\right)}{2}=12\cdot21=252\)
b: 24 đỉnh =>12 đường kính
chọn 1 đường kính =>Sẽ có 22 điểm còn lại
=>Có 22*12=264 tam giác vuông
8 tháng 6 2023
a: Số đường chéo là 24*21/2=21*12=336(đường chéo)
b: Số tam giác vuông tạo thành là:12*22=264 tam giác
9 tháng 6 2023
a. Để tính số đường chéo của một đa giác đều n đỉnh, ta dùng công thức: số đường chéo = n(n-3)/2. Áp dụng vào trường hợp này, ta có số đường chéo của đa giác đều 24 đỉnh là: 24(24-3)/2 = 276 đường chéo.
b. Để lập được một tam giác vuông từ các đỉnh của đa giác đều 24 đỉnh, ta cần chọn 3 đỉnh sao cho 2 trong số đó nằm trên cùng một đường kính của đa giác. Có tổng cộng 24 cách chọn đỉnh trên đường kính và vì mỗi tam giác vuông sẽ được lập bởi 2 đường kính khác nhau, nên số tam giác vuông lập được từ các đỉnh của đa giác đều 24 đỉnh là: 24 x 12 = 288 tam giác vuông. Tuy nhiên, một số tam giác vuông sẽ bị lặp lại khi ta quay đa giác, do đó số tam giác vuông duy nhất là: 288/24 = 12 tam giác vuông.
c. Để lập được một tam giác đều từ các đỉnh của đa giác đều 24 đỉnh, ta cần chọn 3 đỉnh liên tiếp trên đường tròn ngoại tiếp đa giác. Có tổng cộng 24 cách chọn 3 đỉnh liên tiếp, do đó số tam giác đều lập được từ các đỉnh của đa giác đều 24 đỉnh là: 24 tam giác đều.
d. Để lập được một tứ giác từ các đỉnh của đa giác đều 24 đỉnh, ta cần chọn 4 đỉnh bất kỳ. Có tổng cộng C(24,4) cách chọn 4 đỉnh, do đó số tứ giác lập được từ các đỉnh của đa giác đều 24 đỉnh là: C(24,4) = 10626 tứ giác.
e. Để lập được một hình chữ nhật từ các đỉnh của đa giác đều 24 đỉnh, ta cần chọn 4 đỉnh sao cho 2 đỉnh đối diện của hình chữ nhật nằm trên cùng một đường kính của đa giác. Có tổng cộng 24 cách chọn đỉnh trên đường kính và vì mỗi hình chữ nhật sẽ được lập bởi 2 đường kính khác nhau, nên số hình chữ nhật lập được từ các đỉnh của đa giác đều 24 đỉnh là: 24 x 12 = 288 hình chữ nhật. Tuy nhiên, trong số đó có 24 hình vuông, do đó số hình chữ nhật mà không phải là hình vuông là: 288 - 24 = 264 hình chữ nhật.
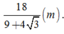
đáp án là
34 hình
19 hình nhưng có thể là có người khác trả lời đúng hơn tôi đấy