Cho x,y nguyên có các tính chất sau:
a)Tổng bình phương của chúng là S
b)Tổng lập phương của chúng bằng T lần tổng của chúng
c)S-T=28
Tìm tất cả các cặp (x;y) (Với x<y)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

tớ chỉ làm phần 1 thôi
1. ta có (x+5)y-x=10
=>(x+5)y-x-5=10-5
=>(x+5)y-(x+5)=5
=>(x+5)(y-1)=5
lập bảng xét giá trị của x,y \(\in Z\)
Bạn tự làm tiếp nhé -_-


Gọi 4 số lập thành cấp số cộng là u1,u2,u3,u4
Ta có:
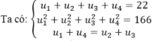
![]()
![]()
Vậy 4 số đó là 1,4,7,10 hoặc 10,7,4,1
Tổng các lập phương của chúng: 13+43+73+ 103=1408
Đáp án là D

Đáp án là D
Gọi 4 số lập thành cấp số cộng là u1,u2,u3,u4 và công sai là d
Ta có: u2 = u1 + d; u3= u1 + 2d; u4 = u1 + 3d
Theo giả thiết ta có:
u
1
+
u
2
+
u
3
+
u
4
=
22
u
1
2
+
u
2
2
+
u
3
2
+
u
4
2
=
166
⇔
u
1
+
u
1
+
d
+
u
1
+
2
d
+
u
1
+
3
d
=
22
u
1
2
+
(
u
1
+
d
)
2
+
(
u
1
+
2
d
)
2
+
(
u
1
+
3
d
)
2
=
166
⇔
4
u
1
+
6
d
=
22
4
u
1
2
+
12
u
1
d
+
14
d
2
=
166
⇒
2
u
1
+
3
d
=
11
(
1
)
2
u
1
2
+
6
u
1
d
+
7
d
2
=
83
(
2
)
Từ (1) suy ra: u 1 = 11 − 3 d 2 thế vào (2) ta được:
2. 11 − 3 d 2 2 + 6. 11 − 3 d 2 . d + 7 d 2 = 83 ⇔ d = 3 ⇒ u 1 = 1 d = − 3 ⇒ u 1 = 10
Vậy 4 số đó là 1,4,7,10 hoặc 10,7,4,1
Tổng các lập phương của chúng:
1 3 + 4 3 + 7 3 + 10 3 = 1408

Gọi hai số đó là a và b. Ta có:
a + b = a . b
Chỉ có đúng một cặp duy nhất .
a = b = 2
\(S=x^2+y^2;\)\(\frac{x^3+y^3}{x+y}=T\)
\(\Rightarrow\left(x^2+y^2\right)-\frac{x^3+y^3}{x+y}=28\)
\(\Leftrightarrow x^2+y^2-\frac{\left(x+y\right)\left(x^2-xy+y^2\right)}{x+y}=28\)
\(\Leftrightarrow xy=28\)
Vì x,y nguyên và x<y nên ta xét từng trường hợp:
Ta được \(\left(x;y\right)=\left(-28;-1\right);\left(-14;-2\right);\left(-7;-4\right);\left(1;28\right);\left(2;14\right);\left(4;7\right)\)