Các bạn giúp mik bài này nữa nhé!!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


e: Ta có: \(\left(x+1\right)\left(x+2\right)=444222\)
\(\Leftrightarrow x^2+3x-444220=0\)
\(\text{Δ}=3^2-4\cdot1\cdot\left(-444220\right)=1776889\)
Vì Δ>0 nên phương trình có hai nghiệm phân biệt là
\(\left\{{}\begin{matrix}x_1=\dfrac{-3-1333}{2}=-668\\x_2=\dfrac{-3+1333}{2}=665\end{matrix}\right.\)

II
1 the most popular
2 more intelligent
3 the shortest
4 bigger than
5 more comfortable than
6 worse
7 more peaceful than
8 the cleverest
9 the most delicious
10 the most boring
11 the most intelligent
12 the oldest
13 more uncomfortable
14 more important
15 healthier
16 the most difficult
17 most expensive
18 faster
19 more interesting
20 earlier
III
1 Gray is taller than Rick
2 John has got new light trousers
3 Mary likes bigger clothes
4 Rick is wearing an expensive coat
5 Carol has got the shortest scraft
6 He is the tallest student
7 Mary was the most ppular actress
8 He was the best football player
9 Mary play better than you
10 Your father is stronger than mine

781 . 152018
781\(\equiv\)( mod 10 )
710\(\equiv\)9 ( mod 10 )
780\(\equiv\)1 ( mod 10 )
781\(\equiv\)7 ( mod 10 )
Vậy chữ số tận cùng của 781 là 1
152018\(\equiv\)( mod 10 )
158\(\equiv\)5 ( mod 10 )
1580\(\equiv\)5 ( mod 10 )
15960\(\equiv\)5 ( mod 10 )
151920\(\equiv\)5 ( mod 10 )
152000\(\equiv\)5 ( mod 10 )
152007\(\equiv\)5 ( mod 10 )
152014\(\equiv\)5 ( mod 10 )
152018\(\equiv\)5 ( mod 10 )
Vậy chữ số tận cùng của 152018 là 5
\(\Rightarrow\)Chữ số tận cùng của 781 . 152018 là 7 . 5 = 35
Vậy chữ số tận cùng của 781 . 152018 là 5
Hk tốt
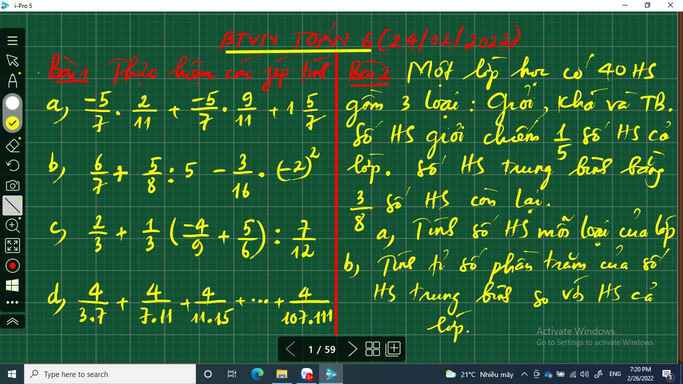
 2 bài này các bạn giúp mik phần d,e,f với
2 bài này các bạn giúp mik phần d,e,f với  còn bài này các bạn giúp mik phần c, h
còn bài này các bạn giúp mik phần c, h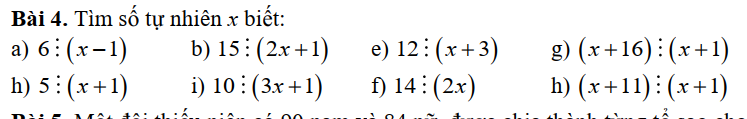 bài này các bạn giúp mik phần g, h, i
bài này các bạn giúp mik phần g, h, i các bạn giúp mik hết luôn hai bài này nhé, mik đang cần cực kì gấp
các bạn giúp mik hết luôn hai bài này nhé, mik đang cần cực kì gấp




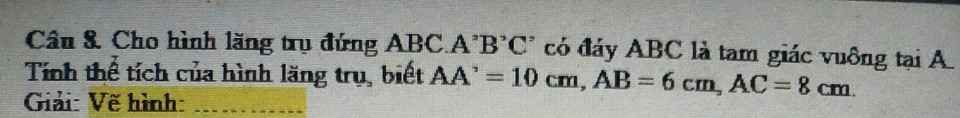
ΔABC cân tại A\(\Rightarrow AB=AC\Rightarrow\dfrac{1}{2}AB=\dfrac{1}{2}AC\Rightarrow AN=NB=AM=MC\)
Xét ΔAMB và Δ ANC có:
\(AM=AN\left(cmt\right)\)
Chung \(\widehat{A}\)
\(AB=AC\left(cmt\right)\)
⇒ΔAMB = Δ ANC (c.g.c)
⇒ BM = CN (2 cạnh tương ứng)
ta có: BN = CM ( ABC cân, BM và CN là trung tuyến )
Xét tam giác BMC và tam giác CNB, có:
CN = CM ( cmt )
góc B = góc C ( ABC cân )
BC: cạnh chung
Vậy tam giác BMC = tam giác CNB ( c.g.c )
=> BM = CN ( 2 cạnh tương ứng )