B O A x y 1 2
Cho $\widehat{AOB}+\widehat{A_2} -180^{\circ} = \widehat{B_1}$. Chứng minh rằng $Ax$ //...
Đọc tiếp
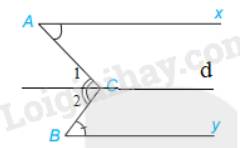
Cho $\widehat{AOB}+\widehat{A_2} -180^{\circ} = \widehat{B_1}$. Chứng minh rằng $Ax$ // $By$.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
3 tháng 7 2023
Vì các tia và ở trong góc nên:
(1)
(2)
Từ (1) và (2), suy ra: .
b) Ta có
c) Từ giả thiết, ta có: .
Mà .
Vậy .
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
29 tháng 11 2023
a/
\(Ax\perp m\left(gt\right);By\perp m\left(gt\right)\) => Ax//By (cùng vuông góc với m)
Mà Cz//Ax (gt)
=> Cz//By (cùng // với Ax)
b/
\(\widehat{BCz}=\widehat{ACB}-\widehat{C}=110^o-30^o=80^o\)
Ta có
Cz//By (cmt) \(\Rightarrow\widehat{BCz}=\widehat{CBy}=80^o\) (góc so le trong)
c/
\(CD\perp Ax\left(gt\right)\Rightarrow\widehat{ADC}=90^o\)
Cz//Ax (gt) \(\Rightarrow\widehat{A}=\widehat{C}=30^o\) (Góc so le trong)
Xét tg vuông ACD có
\(\widehat{ACD}=\widehat{ADC}-\widehat{A}=90^o-30^o=60^o\)
CS
6 tháng 10 2021
a) Ta có: CD//Ey
\(\Rightarrow\widehat{CBE}=\widehat{E_1}=130^0\)(so le trong)
b) Ta có: Ta có: CD//Ey
\(\Rightarrow\widehat{EBD}+\widehat{E_1}=180^0\)(trong cùng phía)
\(\Rightarrow\widehat{EBD}=180^0-\widehat{E_1}=50^0\)
Ta có: \(\widehat{EBD}+\widehat{B_1}=50^0+40^0=90^0\)
=> AB⊥BE
23 tháng 5 2022
cửa hàng bán được một tạ rưỡi gẹo tẻ và gạo nếp ; trong đó 25% là gạo nếp. hỏi của hàng bán mỗi loại bao nhiêu ki-lô-gam gạo
HQ
Hà Quang Minh
Giáo viên
22 tháng 9 2023
a) Ta có: \(\left. \begin{array}{l}OA \bot OB\\OA \bot OC\end{array} \right\} \Rightarrow OA \bot \left( {OBC} \right)\)
Mà \(BC \in \left( {OBC} \right) \Rightarrow OA \bot BC\)
b) Ta có \(\left. \begin{array}{l}OA \bot OB\\OB \bot OC\end{array} \right\} \Rightarrow OB \bot \left( {OAC} \right)\)
Mà \(CA \in \left( {OAC} \right) \Rightarrow CA \bot OB\)
c) Ta có \(\left. \begin{array}{l}OC \bot OB\\OA \bot OC\end{array} \right\} \Rightarrow OC \bot \left( {OAB} \right)\)
Mà \(AB \in \left( {OAB} \right) \Rightarrow AB \bot OC\)
HQ
Hà Quang Minh
Giáo viên
18 tháng 9 2023
a) Xét \(\Delta ABD\) và \(\Delta CBD\)có:
DA=DC(gt)
BD chung
BA=BC
Vậy \(\Delta ABD = \Delta CBD\)(c.c.c)
b) Ta có \(\widehat A = \widehat C = {90^o}\)(hai góc tương ứng)
Theo định lí tổng ba góc trong tam giác BCD, ta có:
\(\begin{array}{l}\widehat C + \widehat {CDB} + \widehat {DBC} = {180^o}\\ \Rightarrow {90^o} + {30^o} + \widehat {DBC} = {180^o}\\ \Rightarrow \widehat {DBC} = {60^o}\end{array}\)
Mà \(\Delta ABD = \Delta CBD\) nên \(\widehat {ABD} = \widehat {CBD}\) ( 2 góc tương ứng)
\(\Rightarrow \widehat {ABD} = \widehat {CBD} = {60^o}\\\Rightarrow \widehat {ABC} = \widehat {ABD} + \widehat {CBD} = {60^o} + {60^o} = {120^o}\)
18 tháng 9 2023
Qua C kẻ đường thẳng d song song với Ax
Vì Ax // By nên d // By
Vì d // Ax nên \(\widehat A = \widehat {{C_1}}\)(2 góc so le trong)
Vì d // By nên \(\widehat B = \widehat {{C_2}}\) (2 góc so le trong)
Mà \(\widehat C = \widehat {{C_1}} + \widehat {{C_2}}\)
Vậy \(\widehat C = \widehat A + \widehat B\)(đpcm)
HQ
Hà Quang Minh
Giáo viên
18 tháng 9 2023
Vì \(\widehat {xAz} = \widehat {yBz}( = 50^\circ )\)
Mà hai góc này ở vị trí đồng vị nên Ax//By (Dấu hiệu nhận biết hai đường thẳng song song)
25 tháng 8 2020
a. Ta có⎪⎨⎪⎩ˆAOD+ˆCOD=90 độ (=ˆAOC)ˆBOC+ˆCOD=90 độ (=ˆBOD)
⇒ˆAOD=ˆBOC
b) Ta có: ⎧⎪⎨⎪⎩ˆAOD+ˆCOD=90 độ (=ˆAOC)ˆBOC+ˆCOD=900 độ (=ˆBOD)
⇒ˆAOD+ˆBOC+ˆCOD+ˆCOD=180 độ
Mà: ˆAOD+ˆBOC+ˆCOD=ˆAOB
⇒ˆAOB+ˆCOD=180 độ
TG
23 tháng 8 2020
a) Ta có: \(\left\{{}\begin{matrix}\widehat{AOD}+\widehat{COD}=90^0\left(=\widehat{AOC}\right)\\\widehat{BOC}+\widehat{COD}=90^0\left(=\widehat{BOD}\right)\end{matrix}\right.\)
\(\Rightarrow\widehat{AOD}=\widehat{BOC}\)
b) Ta có: \(\left\{{}\begin{matrix}\widehat{AOD}+\widehat{COD}=90^0\left(=\widehat{AOC}\right)\\\widehat{BOC}+\widehat{COD}=90^0\left(=\widehat{BOD}\right)\end{matrix}\right.\)
\(\Rightarrow\widehat{AOD}+\widehat{BOC}+\widehat{COD}+\widehat{COD}=180^0\)
Mà: \(\widehat{AOD}+\widehat{BOC}+\widehat{COD}=\widehat{AOB}\)
\(\Rightarrow\widehat{AOB}+\widehat{COD}=180^0\)
Cho \widehat{AOB}+\widehat{A_2} -180^{\circ} = \widehat{B_1}AOB+A2−180∘=B1. Chứng minh rằng AxAx // ByBy.
Hướng dẫn giải:Trong \widehat{A O B}AOB dựng tia O tOt // O xOx. (1)
Suy ra \widehat{O}_{2}+\widehat{A}_{2}=180^{\circ}O2+A2=180∘ (2 góc trong cùng phía).
Khi đó \widehat{O}_{1} =\widehat{A O B}-\widehat{O}_{2} =\widehat{A O B}-\left(180^{\circ}-\widehat{A}_{2}\right) =\widehat{A O B}+\widehat{A}_{2}-180^{\circ} =\widehat{B}_{1}O1=AOB−O2=AOB−(180∘−A2)=AOB+A2−180∘=B1
\Rightarrow O t⇒Ot // B yBy (vì có cặp góc so le trong bằng nhau). (2)
Từ (1) và (2) suy ra A xAx // B yBy (vì cùng song song với O tOt ).
Vậy A tAt // B zBz.