cho tam giác ABC cân tại A .Gọi M là trung điểm của BC
a, Chứng minh AM vuông góc với BC
b , Chứng minh góc BAM = góc CAM
c, Kẻ MH vuông góc với AB tại H ; MK vuông góc với AC tại K chứng minh tam giác MHK cân tại M
d, Chứng minh tam giác AHK cân tại A
e, Chứng minh HK song song với BC

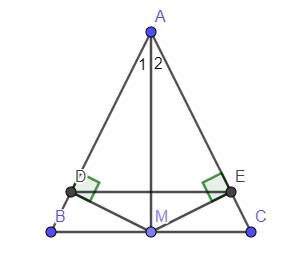
a: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao
b: Ta có: ΔABC cân tại A
mà AM là đường cao
nên AM là tia phân giác của góc BAC
hay góc BAM= góc CAM
c: Xét ΔAHM vuông tại H và ΔAKM vuông tại K có
AM chung
\(\widehat{HAM}=\widehat{KAM}\)
Do đó: ΔAHM=ΔAKM
Suy ra: MH=MK
hay ΔMHK cân tại M
d: Xét ΔAHK có AH=AK
nên ΔAHK cân tại A
e: Xét ΔABC có AH/AB=AK/AC
nên HK//BC