cho tam giác ABC, AD là đường phân giác. Chứng minh rằng : S tam giác ABD/ S tam giác ACD = AB/AC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
3
7 tháng 4 2020
b) xét ∆ABC có AD là đường phân giác của góc A
=>BD/AB=DC/AC ( tính chất)
Áp dụng tính chất dãy tỉ số bằng nhau , được :
BD/AB=DC/AC=BD/6=DC/8=(BD+DC)/(6+8)=BD/14=10/14=5/7
==>BD=6×5:7≈4,3
==>DC=10-4,3≈5,7
3
7 tháng 4 2020
a,Áp dụng định lý Pi-ta-go vào tam giác ABC => tam giác ABC vuông tại A=> AH vuông góc vs BC
=> tam giác ABC đồng dạng vs tam giác HAC ( g.c.g)
b, Vì tam giác ABC vuông tại A nên ta có hệ thức: AC2=BC . HC => đpcm
c, có AD là tia phân giác của tam giác ABC => BD=CD=BC/2= 5cm
CM
29 tháng 3 2019
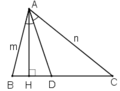
Kẻ AH là đường cao của tam giác ABC
Ta có:
Vậy tỉ số diện tích của tam giác ABD và tam giác ACD bằng m/n.
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
20 tháng 2 2021
a/ Theo tính chất đường phân giác trong tam giác: Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn tỉ lệ với hai cạnh kề của hai đoạn ấy ta có
\(\frac{BD}{CD}=\frac{AB}{AC}=\frac{m}{n}\)
Hai tam giác ABD và tam giác ACD có chung đường cao hạ từ A xuống BC nên
\(\frac{S_{\Delta ABD}}{S_{\Delta ACD}}=\frac{BD}{CD}=\frac{m}{n}\)
b/ Ta có
\(\frac{S_{\Delta ABD}}{S_{\Delta ACD}}=\frac{m}{n}\Rightarrow\frac{S_{\Delta ABD}}{m}=\frac{S_{\Delta ACD}}{n}=\frac{S_{\Delta ABD}+S_{\Delta ACD}}{m+n}=\frac{S_{\Delta ABC}}{m+n}=\frac{s}{m+n}\)
\(\Rightarrow S_{\Delta ABD}=\frac{sm}{m+n}\)
Xét hai tam giác ABM và tam giác ABC có chung đường cao hạ từ A xuống BC nên
\(\frac{S_{\Delta ABM}}{S_{\Delta ABC}}=\frac{BD}{BC}=\frac{1}{2}\Rightarrow S_{\Delta ABM}=\frac{S_{\Delta ABC}}{2}=\frac{s}{2}\)
Mà \(S_{\Delta ADM}=S_{\Delta ABM}-S_{\Delta ABD}=\frac{s}{2}-\frac{sm}{m+n}\)
2 tháng 1 2022
a: Xét ΔABD vuông tại B và ΔACD vuông tại C có
AD chung
AB=AC
Do đó; ΔABD=ΔACD
2 tháng 1 2022
a: Xét ΔABD vuông tại B và ΔACD vuông tại C có
AD chung
AB=AC
Do đó: ΔABD=ΔACD
25 tháng 4 2023
a: Xét ΔABD và ΔACD có
AB=AC
góc BAD=góc CAD
AD chung
=>ΔABD=ΔACD
c: ΔABC cân tại A
mà AD là phân giác
nen AD vuông góc BC
Xét ΔABC có
AD,BE,CK là các đường cao
=>AD,BE,CK đồng quy
NY
1 tháng 4 2020
a) Xét \(\Delta\)ABD và \(\Delta\)ACD có:
AB = AC (gt)
AD: cạnh chung
BD = CD (D là trung điểm của BC)
\(\Rightarrow\Delta\)ABD = \(\Delta\)ACD (c.c.c)
b) Ta có: \(\Delta\)ABD = \(\Delta\)ACD (theo ý a)
\(\Rightarrow\widehat{BAD}\) = \(\widehat{CAD}\) (2 góc tương ứng)
\(\Rightarrow\) AD là tia phân giác của \(\widehat{BAC}\)
c) Ta có: \(\Delta\)ABD = \(\Delta\)ACD (theo ý a)
\(\Rightarrow\widehat{ADB}\) =\(\widehat{ADC}\) (2 góc tương ứng)
mà \(\widehat{ADB}\) + \(\widehat{ADC}\) = 18001800 (2 góc kề bù)
\(\Rightarrow\widehat{ADB}\) = \(\widehat{ADC}\) = 900900
\(\Rightarrow\) AD \(\perp\) BC
Lại có: d // BC (gt) \(\Rightarrow\) AD \(\perp\) d
ĐS:......................
#Châu's ngốc
Từ A kẻ đường cao AH, H thuộc BC.
Xét \(\Delta ABC:\) AD là đường phân giác (gt).
\(\Rightarrow\dfrac{AB}{AC}=\dfrac{BD}{DC}\) (Tính chất đường phân giác).
Ta có:
\(S_{\Delta ABD}=\dfrac{1}{2}.AH.BD.\\ S_{\Delta ACD}=\dfrac{1}{2}.AH.DC.\\ \Rightarrow\dfrac{S_{\Delta ABD}}{S_{\Delta ACD}}=\dfrac{\dfrac{1}{2}.AH.BD}{\dfrac{1}{2}.AH.DC}=\dfrac{BD}{DC}.\)
Mà \(\dfrac{AB}{AC}=\dfrac{BD}{DC}\left(cmt\right).\)
\(\Rightarrow\dfrac{S_{\Delta ABD}}{S_{\Delta ACD}}=\dfrac{AB}{AC}.\)