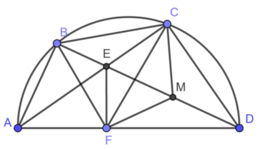
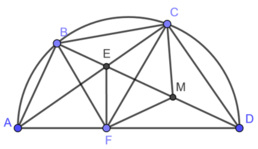
Cho tứ giác ABCD có hai đỉnh B và C ở trên nửa đường tròn đường kính AD,tâm O.Hai đường chéo AC và BD cắt nhau tại E.Gohi H là hình chiếu vuông góc của E xuống AD và I là trung điểm của DE.cmr
a,Các tứ giác ABEH,DCEH nội tiếp được đường tròn
b,E là tâm đường tròn nội tiếp tam giác BCH
Năm điêm B,C,I,O,H cùng thuộc 1 đường tròn
Ai giúp t câu 3 vs


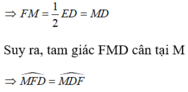
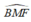 là góc ngoài tại đỉnh M của tam giác FMD nên:
là góc ngoài tại đỉnh M của tam giác FMD nên:
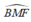 và
và 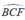 và cùng nhìn cạnh BF dưới một góc bằng nhau
và cùng nhìn cạnh BF dưới một góc bằng nhau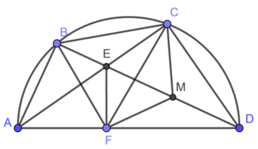


Để chứng minh 5 điểm trên cùng thuộc một đường tròn, ta chứng minh góc BCH = góc BIH = góc BOH.
Thật vậy, theo chứng minh b, E là tâm đường tròn nội tiếp tam giác BCH nên CE là phân giác góc BCH. Từ đó góc BCH = 2 góc BCA.
Ta có góc BCA bằng góc BDA vì cùng chắn cung BA, nên góc BCH = 2 góc BDA (1)
Tam giác OBD cân tại O nên BOH = 2 góc BDA.(2)
Tam giác EHD vuông tại H , HI là trung tuyến ứng với cạnh huyền nên IH = ID, từ đó góc BIH = 2 góc BDA.(3)
Từ (1), (2), (3) ta suy ra 3 góc trên bằng nhau hay 5 điểm B, C, I, O, H cùng thuộc một đường tròn.