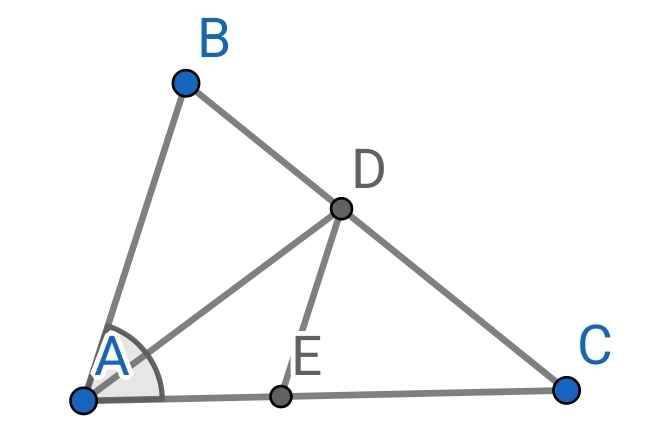
cho ΔABC ⊥ tại A có AB=21cm, AC=28cm. AD phân giác ∠BAC (D ∈ BC)
a)tính DB, DC
b) kẻ DE ⊥ AC. Tính DE, EC
c)c/m: ΔABC∼ΔEDC. Hãy tính tỉ số đồng dạng
d) gọi I là giao điểm các đg phân giác và G là trọng tâm ΔABC, c/m IG//AC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
21 tháng 2 2022
c: Xét ΔABC vuông tại A và ΔEDC vuông tại E có
\(\widehat{C}\) chung
Do đó: ΔABC∼ΔEDC
a: BC=35cm
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{BD}{21}=\dfrac{CD}{28}=\dfrac{BD+CD}{21+28}=\dfrac{35}{49}=\dfrac{5}{7}\)
Do đó:BD=15cm; CD=20cm
21 tháng 2 2022
d) -BG, BI cắt AC lần lượt tại H,F.
-Xét △ABC có:
I, G lần lượt là giao các đường phân giác và trọng tâm (gt).
\(\Rightarrow\)BI, BG lần lượt là phân giác, trung tuyến của △ABC.
Mà -BI, BG cắt AC lần lượt tại F,H (gt).
AD phân giác \(\widehat{BAC}\) (D∈BC) (gt).
\(\Rightarrow\dfrac{BG}{BH}=\dfrac{2}{3}\); BF là phân giác của \(\widehat{ABC}\).
I∈AD.
-Xét △ABC có: BF là phân giác của \(\widehat{ABC}\) (cmt).
\(\Rightarrow\dfrac{AB}{BC}=\dfrac{AF}{FC}\) (định lí đường phân giác trong tam giác).
\(\Rightarrow\dfrac{AF}{AB}=\dfrac{FC}{BC}=\dfrac{AF+FC}{AB+BC}=\dfrac{AC}{AB+BC}=\dfrac{28}{21+35}=\dfrac{1}{2}\)
-Xét △ABF có: AI là phân giác của \(\widehat{BAC}\)
\(\Rightarrow\dfrac{AF}{AB}=\dfrac{IF}{BI}=\dfrac{1}{2}\) (định lí đường phân giác trong tam giác).
\(\Rightarrow IF=\dfrac{1}{2}BI\) mà \(IF+BI=BF\)
\(\Rightarrow\dfrac{1}{2}BI+BI=BF\)
\(\Rightarrow\dfrac{3}{2}BI=BF\)
\(\Rightarrow BI=\dfrac{2}{3}BF\)
-Xét △BFH có: \(\dfrac{BI}{BF}=\dfrac{BG}{BH}\left(=\dfrac{2}{3}\right)\)
\(\Rightarrow\)IG//FH (định lí Ta-let đảo) nên IG//AC
7 tháng 3 2022
a: BC=35cm
Xét ΔABC có AD là phân giác
nên BD/AB=CD/AC
=>BD/3=CD/4
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{BD}{3}=\dfrac{CD}{4}=\dfrac{BD+CD}{3+4}=\dfrac{35}{7}=5\)
Do đó:BD=15cm; CD=20cm
b: Xét ΔABC có DE//AB
nên DE/AB=CD/BC
=>DE/21=20/35=4/7
=>DE=12cm
Xét ΔABC cso DE//BC
nên CE/CA=ED/AB
=>CE/28=12/21=4/7
=>CE=12cm
NB
7 tháng 3 2022
e tự vẽ hình nha
a) vì tg ABC vg tại A(gt)
\(\Rightarrow AB^2+AC^2=BC^2\left(pytago\right)\\ \Leftrightarrow28^2+21^2=BC^2\\ \Leftrightarrow BC=35\left(cm\right)\)
có AD là pgiac(gt)
\(\Rightarrow\dfrac{BD}{CD}=\dfrac{AB}{AC}=\dfrac{21}{28}\\ \Leftrightarrow\dfrac{BD}{21}=\dfrac{CD}{28}=\dfrac{BD+CD}{21+28}=\dfrac{BC}{49}=\dfrac{35}{49}\)
\(+\dfrac{BD}{21}=\dfrac{35}{49}\Rightarrow BD=15\left(cm\right)\\ +\dfrac{CD}{28}=\dfrac{35}{49}\Rightarrow CD=20\left(cm\right)\)
b) xét tgiac ABC và tgac EDC có:
+ góc C chung
+ góc E = góc A (=90 độ)
+ góc D = góc B ( sltrong, DE//AB vì cùng vg góc AC)
\(\Rightarrow\Delta ABC\sim\Delta EDC\left(ggg\right)\\ \Rightarrow\dfrac{CB}{CD}=\dfrac{AB}{ED}=\dfrac{AC}{EC}\)
\(\Leftrightarrow\dfrac{35}{20}=\dfrac{AB}{ED}=\dfrac{AC}{EC}\)
\(+ED=\dfrac{20.21}{35}=12\left(cm\right)\\ +EC=\dfrac{28.20}{35}=16\left(cm\right)\)
c) ở trên câu b a làm có luôn tam giác với tỉ số r đấy e chép xuống
24 tháng 2 2022
a: BC=10cm
Xét ΔABC có AD là phân giác
nên BD/CD=AB/AC=3/4
=>BD/3=CD/4
Áp dụng tính chất của dãy tỉ số bằng nhau,ta được:
\(\dfrac{BD}{3}=\dfrac{CD}{4}=\dfrac{BD+CD}{3+4}=\dfrac{10}{7}\)
Do đó: BD=30/7(cm); CD=40/7(cm)
b: Xét ΔABC có DE//AC
nên DE/AC=BD/BC
=>\(\dfrac{DE}{8}=\dfrac{30}{7}:10=\dfrac{3}{7}\)
=>DE=24/7(cm)
9 tháng 3 2023
a: \(BC=\sqrt{21^2+28^2}=35\left(cm\right)\)
AD là phân giác
=>DB/AB=DC/AC
=>DB/3=DC/4=(DB+DC)/(3+4)=35/7=5
=>DB=15cm; DC=20cm
b: Xét ΔCAB có DE//AB
nên DE/AB=CD/CB=CE/CA
=>CE/28=DE/21=20/35=4/7
=>CE=16cm; DE=12cm
22 tháng 1
a: Ta có: ΔABC vuông tại A
=>\(BC^2=AB^2+AC^2\)
=>\(BC^2=25+49=74\)
=>\(BC=\sqrt{74}\left(cm\right)\)
Xét ΔABC có AD là phân giác
nên \(\dfrac{DB}{AB}=\dfrac{DC}{AC}\)
=>\(\dfrac{DB}{5}=\dfrac{DC}{7}\)
mà \(DB+DC=BC=\sqrt{74}\)
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{DB}{5}=\dfrac{DC}{7}=\dfrac{DB+DC}{5+7}=\dfrac{\sqrt{74}}{12}\)
=>\(DB=\dfrac{\sqrt{74}}{12}\cdot5=\dfrac{5\sqrt{74}}{12}\left(cm\right);DC=\dfrac{7\sqrt{74}}{12}\left(cm\right)\)
b: Xét ΔCAB có ED//AB
nên \(\dfrac{CE}{CA}=\dfrac{CD}{CB}=\dfrac{ED}{AB}\)
=>\(\dfrac{CE}{7}=\dfrac{ED}{5}=\dfrac{7\sqrt{74}}{12}:\sqrt{74}=\dfrac{7}{12}\)
=>\(CE=\dfrac{7}{12}\cdot7=\dfrac{49}{12}\left(cm\right);ED=7\cdot\dfrac{5}{12}=\dfrac{35}{12}\left(cm\right)\)
c: Xét ΔABC vuông tại A và ΔEDC vuông tại E có
\(\widehat{ACB}\) chung
Do đó: ΔABC~ΔEDC
=>\(k=\dfrac{BC}{DC}=\sqrt{74}:\dfrac{7\sqrt{74}}{12}=\dfrac{12}{7}\)
2 tháng 4 2021
a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=21^2+28^2=1225\)
hay BC=35(cm)
Xét ΔABC có AD là đường phân giác ứng với cạnh BC(gt)
nên \(\dfrac{BD}{AB}=\dfrac{CD}{AC}\)(Tính chất đường phân giác của tam giác)
hay \(\dfrac{BD}{21}=\dfrac{CD}{28}\)
mà BD+CD=BC(D nằm giữa B và C)
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{BD}{21}=\dfrac{CD}{28}=\dfrac{BD+CD}{21+28}=\dfrac{BC}{49}=\dfrac{35}{49}=\dfrac{5}{7}\)
Do đó:
\(\left\{{}\begin{matrix}\dfrac{BD}{21}=\dfrac{5}{7}\\\dfrac{CD}{28}=\dfrac{5}{7}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BD=15\left(cm\right)\\CD=20\left(cm\right)\end{matrix}\right.\)
Vậy: BD=15cm; CD=20cm
25 tháng 2 2022
-Tham khảo:
https://hoc24.vn/cau-hoi/giup-2-cau-cuoi-thoicho-dabc-tai-a-co-ab21cm-ac28cm-ad-phan-giac-bac-d-bcatinh-db-dcb-ke-de-ac-tinh-de-ecccm-dabcdedc-hay-tinh.4844365471752
KV
19 tháng 11 2023
a) Do AD là đường phân giác của ∆ABC (gt)
⇒ BD/AB = CD/AC
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
BD/AB = CD/AC = (BD + CD)/(AB + AC) = BC/(12 + 20) = 28/32 = 7/8
BD/AB = 7/8 ⇒ BD = AB.7/8 = 12.7/8 = 10,5 (cm)
⇒ CD = BC - BD = 28 - 10,5 = 17,5 (cm)
b) ∆ABC có:
DE // AB
⇒ DE/AB = CD/BC
⇒ DE/12 = 17,5/28
⇒ DE = 12 . 17,5/28 = 7,5 (cm)
a: BC=35cm
Xét ΔABC có AD là phân giác
nên BD/AB=CD/AC
=>BD/21=CD/28
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{BD}{21}=\dfrac{CD}{28}=\dfrac{BD+CD}{21+28}=\dfrac{35}{49}=\dfrac{5}{7}\)
Do đó:BD=15cm; CD=20cm
b: Xét ΔABC có DE//AB
nên DE/AB=CD/CB
=>DE/21=20/35=4/7
=>DE=12(cm)
Xét ΔABC có ED//AB
nên CE/CA=ED/AB
=>CE/28=12/21=4/7
=>CE=12(cm)