Ai biết giúp mình bài 2,3,4 với ạ mình cần gấp
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.





\(1,\\ a,M=\sqrt{3}-1-6\sqrt{3}+\sqrt{3}+1=-4\sqrt{3}\\ b,ĐK:x\ge1\\ PT\Leftrightarrow3\sqrt{x-1}-\sqrt{x-1}=1\Leftrightarrow\sqrt{x-1}=\dfrac{1}{2}\\ \Leftrightarrow x-1=\dfrac{1}{4}\Leftrightarrow x=\dfrac{5}{4}\left(tm\right)\\ 2,\\ a,ĐK:x>0;x\ne1\\ P=\dfrac{x-1}{\sqrt{x}\left(\sqrt{x}-1\right)}:\dfrac{\sqrt{x}-1+2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\\ P=\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}-1\right)}\cdot\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\sqrt{x}+1}=\dfrac{x-1}{\sqrt{x}}\\ b,P< 0\Leftrightarrow x-1< 0\left(\sqrt{x}>0\right)\\ \Leftrightarrow0< x< 1\\ c,P\sqrt{x}=m-\sqrt{x}\\ \Leftrightarrow x-1=m-\sqrt{x}\\ \Leftrightarrow x+\sqrt{x}-m-1=0\\ \text{PT có nghiệm nên }\Delta=1+4\left(m+1\right)\ge0\\ \Leftrightarrow4m+5\ge0\Leftrightarrow m\ge-\dfrac{5}{4}\)

Bài 1:
a, \(\)\(\)\(=>R2//\left[R4nt\left(R3//R5\right)\right]\)
\(=>Rtd=\dfrac{R2\left[R4+\dfrac{R3.R5}{R3+R5}\right]}{R2+R4+\dfrac{R3.R5}{R3+R5}}=\dfrac{1.\left[1+\dfrac{1}{1+1}\right]}{1+1+\dfrac{1}{1+1}}=0,6\left(ôm\right)\)
\(=>I=\dfrac{Uab}{Rtd}=\dfrac{10}{0,6}=\dfrac{50}{3}A=I1\)
\(=>Uab=U2345=10V=U2=U345\)
\(=>I2=\dfrac{U2}{R2}=\dfrac{10}{1}=10A\)
\(=>I345=\dfrac{U345}{R345}=\dfrac{10}{1+\dfrac{1.1}{1+1}}=\dfrac{20}{3}A=I4=I35\)
\(=>U35=I35.R35=\dfrac{20}{3}.\dfrac{1.1}{1+1}=\dfrac{10}{3}V=U3=U5\)
\(=>I3=\dfrac{U3}{R3}=\dfrac{\dfrac{10}{3}}{1}=\dfrac{10}{3}A,\)
\(=>I5=\dfrac{U5}{R5}=\dfrac{10}{3}A\)
b, \(I1=0,1A=Im=I2345\)
\(=>Uab=I2345.R2345=0,1.\dfrac{6\left[8+\dfrac{6.12}{6+12}\right]}{6+8+\dfrac{6.12}{6+12}}=0,4V\)

Bài 8:
\(1,P=\dfrac{x+3\sqrt{x}+2+2x-4\sqrt{x}-2-5\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{3x-6\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\\ P=\dfrac{3\sqrt{x}\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{3\sqrt{x}}{\sqrt{x}+2}\\ 2,P=2\Leftrightarrow2\sqrt{x}+4=3\sqrt{x}\Leftrightarrow\sqrt{x}=4\\ \Leftrightarrow x=16\left(tm\right)\)
Bài 9:
\(a,M=\dfrac{x-1}{\sqrt{x}\left(\sqrt{x}-1\right)}:\dfrac{\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\\ M=\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}-1\right)}\cdot\left(\sqrt{x}-1\right)\\ M=\dfrac{x-1}{\sqrt{x}}\\ b,M>0\Leftrightarrow x-1>0\left(\sqrt{x}>0\right)\\ \Leftrightarrow x>1\)
Bài 10:
\(a,A=\dfrac{\sqrt{\left(x+3\right)^2}}{x+3}=\dfrac{\left|x+3\right|}{x+3}\)
Với \(x\ge-3\Leftrightarrow A=\dfrac{x+3}{x+3}=1\)
Với \(x< -3\Leftrightarrow A=\dfrac{-\left(x+3\right)}{x+3}=-1\)
\(b,B=\dfrac{2}{x-1}\cdot\dfrac{\left|x-1\right|}{2\left|x\right|}\)
Với \(0< x< 1\Leftrightarrow B=\dfrac{2}{x-1}\cdot\dfrac{-\left(x-1\right)}{2x}=-\dfrac{1}{x}\)


\(\dfrac{3}{1^2.2^2}+\dfrac{5}{2^2.3^2}+...+\dfrac{19}{9^2.10^2}\)
=\(\dfrac{3}{1.4}+\dfrac{5}{4.9}+...+\dfrac{19}{81.100}\)
=\(1-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{9}+...+\dfrac{1}{81}-\dfrac{1}{100}\)
=\(1-\dfrac{1}{100}=\dfrac{99}{100}\)
Mà \(\dfrac{99}{100}< 1\) nên \(\dfrac{3}{1^2.2^2}+\dfrac{5}{2^2.3^2}+...+\dfrac{19}{9^2.10^2}< 1\)



 ai giúp mình bài 3 với ạ, mình đang cần gấp, mình cảm ơn
ai giúp mình bài 3 với ạ, mình đang cần gấp, mình cảm ơn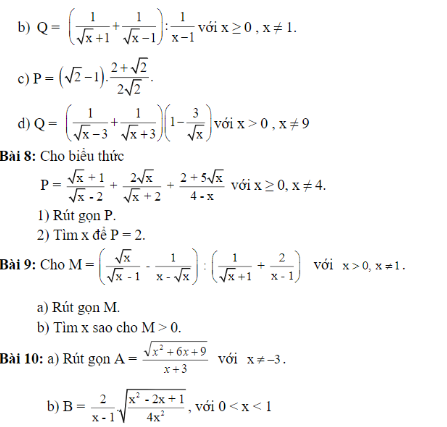




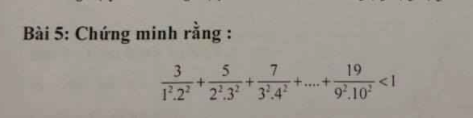 đang cần gấp bài 5 ai giúp mình với ạ :))
đang cần gấp bài 5 ai giúp mình với ạ :))