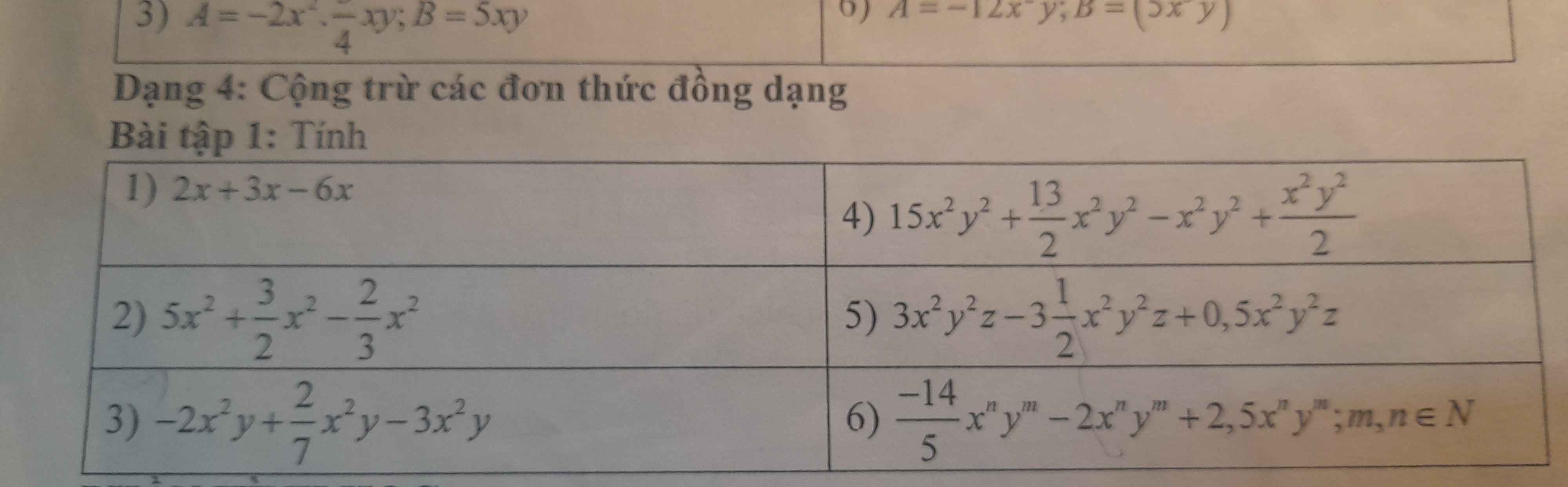Giúp em bài 4,5,6 vs ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
10 tháng 12 2023
Bài 4:
a. Khi $m=2$ thì hàm số là: $y=x+2$.
Cho $x=0$ thì $y=x+2=0+2=2$. Ta có điểm $(0,2)$
Cho $x=1$ thì $y=1+2=3$. Ta có điểm $(1,3)$
Nối $(0,2)$ với $(1,3)$ ta được đths $y=x+2$
b.
Để hàm đồng biến thì $m^2-3>0$
$\Leftrightarrow m> \sqrt{3}$ hoặc $m< -\sqrt{3}$
Để hàm nghịch biến thì $m^2-3<0$
$\Leftrightarrow -\sqrt{3}< m< \sqrt{3}$
c.
Để $(d)$ đi qua $A(1;2)$ thì:
$y_A=(m^2-3)x_A+2$
$\Leftrightarrow 2=(m^2-3).1+2=m^2-1$
$\Leftrightarrow m^2=3\Leftrightarrow m=\pm \sqrt{3}$
d. Để $(d)$ đi qua $B(1;8)$ thì:
$y_B=(m^2-3)x_B+2$
$\Leftrightarrow 8=(m^2-3).1+2=m^2-1$
$\Leftrightarrow m^2=9\Leftrightarrow m=\pm 3$
AH
Akai Haruma
Giáo viên
10 tháng 12 2023
Bài 6:
$M$ nằm trên đường thẳng $2x+y=3$ nên:
$2x_M+y_M=3$
Mà $x_M=\frac{1}{2}$ nên $y_M=3-2x_M=3-2.\frac{1}{2}=2$
Vậy $M(\frac{1}{2};2)$
Gọi PTĐT $(d)$ là $y=ax+b$
$A(-2;1)\in (d)$ nên: $y_A=ax_A+b$
$\Rightarrow 1=-2a+b(1)$
$M(\frac{1}{2};2)\in (d)$ nên:
$y_M=ax_M+b$
$\Rightarrow 2=\frac{1}{2}a+b(2)$
Từ $(1); (2)\Rightarrow a=\frac{2}{5}; b=\frac{9}{5}$
$\Rightarrow (d): y=\frac{2}{5}x+\frac{9}{5}$
30 tháng 1 2022
1, \(2x+3x-6x=-x\)
2, \(5x^2+\dfrac{3}{2}x^2-\dfrac{2}{3}x^2=\dfrac{35}{6}x^2\)
3, \(-2x^2y+\dfrac{2}{7}x^2y-3x^2y=-\dfrac{33}{7}x^2y\)
4, \(15x^2y^2+\dfrac{13}{2}x^2y^2-x^2y^2+\dfrac{x^2y^2}{2}=21x^2y^2\)
5, \(-\dfrac{14}{5}x^ny^m-2x^ny^m+2,5x^ny^m=-\dfrac{23}{10}x^ny^m\)
30 tháng 1 2022
mình thiếu câu 5 :v câu 5 bài trước là câu 6 nhé
\(3x^2y^2z-\dfrac{7}{2}x^2y^2z+\dfrac{1}{2}x^2y^2z=0\)
12 tháng 3 2022
Bài 5:
a: \(=4x^2y^3\)
b: \(=\dfrac{9}{2}x^2y\)
c: \(=xyz^2\left(\dfrac{3}{4}-\dfrac{1}{4}+\dfrac{1}{2}\right)=xyz^2\)
12 tháng 3 2022
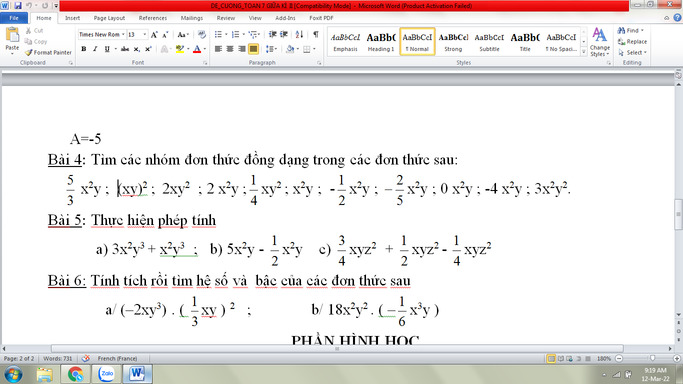
Bài 4
Nhóm 1: \(\dfrac{5}{3}x^2y,2x^2y,x^2y,\dfrac{1}{2}x^2y,\dfrac{-1}{2}x^2y,\dfrac{-2}{5}x^2y,0x^2y,-4x^2y\)
Nhóm 2: \(\left(xy\right)^2,3x^2y^2\)
Bài 5
\(a,3x^2y^3+x^2y^3\)
\(=4x^2y^3\)
\(b,5x^2y-\dfrac{1}{2}x^2y\)
\(=\left(5-\dfrac{1}{2}\right)\left(x^2y\right)\)
\(=\dfrac{9}{2}x^2y\)
\(c,\dfrac{3}{4}xyz^2+\dfrac{1}{2}xyz^2-\dfrac{1}{4}xyz^2\)
\(=\left(\dfrac{3}{4}+\dfrac{1}{2}-\dfrac{1}{4}\right)\left(xyz^2\right)\)
\(=\left(\dfrac{3}{4}+\dfrac{2}{4}-\dfrac{1}{4}\right)\left(xyz^2\right)\)
\(=xyz^2\)
Bài 6
\(a,\left(-2xy^3\right)\left(\dfrac{1}{3}xy\right)^2\)
\(=\left(-2.\dfrac{1}{9}\right)\left(x.x^2\right)\left(y^3y^2\right)\)
\(=\dfrac{-2}{9}x^3y^5\)
Bậc: 3 + 5 = 8
Hệ số: \(\dfrac{-2}{9}\)
\(b,18x^2y^2\left(\dfrac{-1}{6}x^3y\right)\)
\(=\left(-18.\dfrac{1}{6}a\right)\left(x^2x^2\right)\left(y^2y^3\right)\)
\(=-3ax^4y^5\)
Bậc: 4 + 5 = 9
Hệ số: \(-3a\)
NB
7 tháng 9 2023
Để tính quãng đường đi được từ thời điểm t1 đến t2 cho vật giao động điều hòa dọc theo trục Ox, ta cần tính diện tích dưới đường cong x(t) trong khoảng thời gian từ t1 đến t2.
Trước tiên, chúng ta sẽ tính x(t) tại t1 và t2:
Tại t1 = 13/6 s: x(t1) = 3 * cos(4 * 3.14 - (3.14 / 3)) cm
Tại t2 = 23/6 s: x(t2) = 3 * cos(4 * 3.14 - (3.14 / 3)) cm
Tiếp theo, chúng ta cần tính diện tích dưới đường cong trong khoảng từ t1 đến t2. Để làm điều này, ta sẽ tính diện tích của hình giữa đồ thị và trục Ox trong khoảng từ t1 đến t2.
Diện tích A = ∫(t1 đến t2) x(t) dt
A = ∫(13/6 đến 23/6) [3 * cos(4 * 3.14 - (3.14 / 3))] dt
A = ∫(13/6 đến 23/6) [3 * cos(4 * 3.14 - 3.14/3)] dt
A = ∫(13/6 đến 23/6) [3 * cos(4 * 3.14 - 3.14/3)] dt
A = ∫(13/6 đến 23/6) [3 * cos(12.56 - 1.0467)] dt
A = ∫(13/6 đến 23/6) [3 * cos(11.5133)] dt
Giải tích phần này trở nên phức tạp, nhưng bạn có thể tính toán nó bằng máy tính hoặc phần mềm tính toán. Kết quả sẽ là diện tích A, tức là quãng đường đi được từ t1 đến t2.
(em thay pi=3,14 luôn nha anh )
TN
1
10 tháng 1 2022
a/ Tam giác AMN cân tại A (gt). \(\Rightarrow\) \(\widehat{AMN}=\widehat{ANM};AM=AN.\)
Xét tam giác AMB và tam giác ANC có:
+ AM = AN (cmt).
+ \(\widehat{AMB}=\widehat{ANC}\left(\widehat{AMN}=\widehat{ANM}\right).\)
+ MB = NC (gt).
\(\Rightarrow\) Tam giác AMB = Tam giác ANC (c - g - c).
\(\Rightarrow\) AB = AC (cặp cạnh tương ứng).
Xét tam giác ABC có: AB = AC (cmt).
\(\Rightarrow\) Tam giác ABC cân tại A.
b/ Tam giác ABC cân tại A (cmt) \(\Rightarrow\) \(\widehat{ABC}=\widehat{ACB}.\)
Mà \(\widehat{ABC}=\widehat{MBH;}\widehat{ACB}=\widehat{NCK}\text{}\) (đối đỉnh).
\(\Rightarrow\) \(\widehat{MBH}=\widehat{NCK}.\)
Xét tam giác MBH và tam giác NCK \(\left(\widehat{BHM}=\widehat{CKN}=90^o\right)\)có:
+ MB = NC (gt).
+ \(\widehat{MBH}=\widehat{NCK}\left(cmt\right).\)
\(\Rightarrow\) Tam giác MBH = Tam giác NCK (cạnh huyền - góc nhọn).
c/ Tam giác MBH = Tam giác NCK (cmt).
\(\Rightarrow\) \(\widehat{BMH}=\widehat{CNK}\) (cặp góc tương ứng).
Xét tam giác OMN có: \(\widehat{NMO}=\widehat{MNO}\) (do \(\widehat{BMH}=\widehat{CNK}\)).
\(\Rightarrow\) Tam giác OMN tại O.
6 tháng 1 2022
Câu 2:
1: \(\Leftrightarrow x\cdot\dfrac{7}{2}=\dfrac{9}{2}+3=\dfrac{15}{2}\)
hay x=15/7
2: \(\Leftrightarrow x=\dfrac{5}{2}\cdot\dfrac{8}{5}=4\)
3: \(\Leftrightarrow x=\dfrac{-11\cdot10}{5}=-11\cdot2=-22\)
4: =>2x=90
hay x=45