Cho bất phương trình x2-6x +2(m+2)|x-3| +m2 +4m +12 >0
có bao nhiêu giá trị nguyên của m ϵ [-10;10] để bất phương tình đúng với mọi xϵ (-2;5)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đặt ![]()
Suy ra ![]()
Ta có ![]()
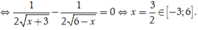
Ta có bảng biến thiên
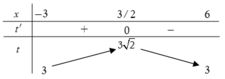
Từ bảng biến thiên ta suy ra ![]()
Khi đó bất phương trình trở thành: ![]()
![]()
Xét hàm số ![]() với
với ![]()
Ta có ![]()
Suy ra hàm số f(t) nghịch biến trên ![]()
![]()
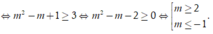
Chọn C.

a.
Pt có 2 nghiệm pb khi:
\(\left\{{}\begin{matrix}m+1\ne0\\\Delta'=\left(m+3\right)^2-\left(m+1\right)\left(-m+2\right)>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ne-1\\2m^2+7m+7>0\left(\text{luôn đúng}\right)\end{matrix}\right.\)
\(\Rightarrow m\ne-1\)
b.
BPT vô nghiệm khi \(\left(m^2-4m-5\right)x^2+2\left(m-5\right)-1< 0\) nghiệm đúng với mọi x
- Với \(m=-1\) ko thỏa mãn
- Với \(m=5\) thỏa mãn
- Với \(m\ne\left\{-1;5\right\}\)
\(\Rightarrow\left\{{}\begin{matrix}m^2-4m-5< 0\\\Delta'=\left(m-5\right)^2+m^2-4m-5< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-1< m< 5\\\left(m-5\right)\left(2m-4\right)< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-1< m< 5\\2< m< 5\end{matrix}\right.\) \(\Rightarrow2< m< 5\)
Kết hợp lại ta được: \(2< m\le5\)

Chọn C
![]()
![]()
![]()
![]()
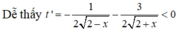
nên hàm t = t (x) nghịch biến trên (-2;2)
![]()
![]()
Thay vào bất phương trình trên được:
![]()
![]()
Bất phương trình đã cho nghiệm đúng với mọi x ∈ - 2 ; 2 nếu và chỉ nếu bất phương trình
![]()
nghiệm đúng với mọi t ∈ - 6 ; 2
tam thức bậc hai f t = 2 t 2 - m t + 3 m - 5 có hai nghiệm thỏa mãn
![]()
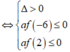
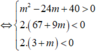
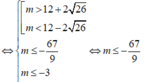
Kết hợp với m ∈ - 10 ; 10 thì m ∈ - 10 ; - 9 ; - 8

2 x 2 – (4m + 3)x + 2 m 2 – 1 = 0 (2)
Phương trình (2) có nghiệm khi và chỉ khi ∆ ≥ 0
Ta có: ∆ = - 4 m + 3 2 – 4.2(2 m 2 – 1)
= 16 m 2 + 24m + 9 – 16 m 2 + 8 = 24m + 17
∆ ≥ 0 ⇔ 24m + 17 ≥ 0 ⇔ m ≥ -17/24
Vậy khi m ≥ -17/24 thì phương trình đã cho có nghiệm.
Giải phương trình (2) theo m:


\(a.\Leftrightarrow mx^2+2mx-x+m+2=0\)
\(\Leftrightarrow mx\left(x+2\right)+\left(m+2\right)-x=0\)
\(\Leftrightarrow\left(m+2\right)\left(mx+1\right)-x=0\)
\(\Rightarrow\left\{{}\begin{matrix}m=\left(0+x\right):\left(mx+1\right)-2\\m=[\left(0+x\right):\left(m+2\right)-1]:x\end{matrix}\right.\)

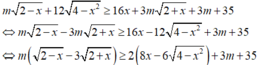

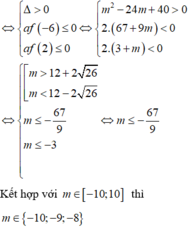
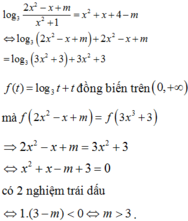
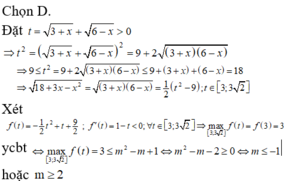
\(\Leftrightarrow\left(x-3\right)^2+2\left(m+2\right)\left|x-3\right|+m^2+4m+3>0\)
Đặt \(\left|x-3\right|=t\Rightarrow0\le t< 5\)
\(\Rightarrow t^2+2\left(m+2\right)t+m^2+4m+3>0\) ;\(\forall t\in[0;5)\)
\(\Leftrightarrow\left(t+m+1\right)\left(t+m+3\right)>0\)
\(\Rightarrow-m-3< t< -m-1\)
Pt nghiệm đúng với mọi \(t\in[0;5)\) khi và chỉ khi
\(\left\{{}\begin{matrix}0>-m-3\\5\le-m-1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m>-3\\m\le-5\end{matrix}\right.\)
\(\Rightarrow\) Không tồn tại m thỏa mãn
Chỗ này mà không phân tích được thành nhân tử thì làm cách phương trình \(f\left(t\right)=0\) có nghiệm thỏa mãn \(t_1\le0< 5< t_2\) đúng không ạ.