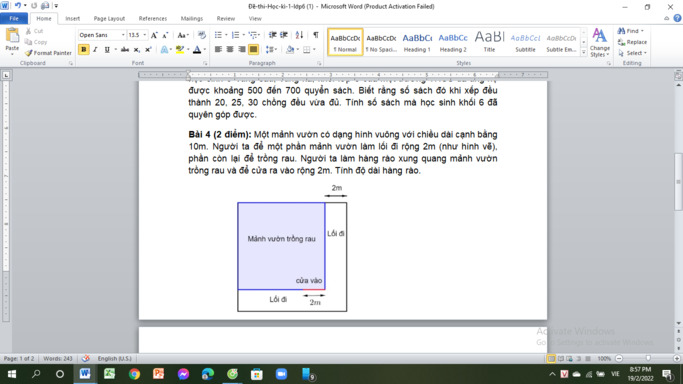
giúp làm bài 4 với
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
4 tháng 10 2021
3: Ta có: ΔABC vuông tại A
nên \(\widehat{B}+\widehat{C}=90^0\)
hay \(\widehat{B}=60^0\)
Xét ΔABC vuông tại A có
\(\sin\widehat{C}=\dfrac{AB}{BC}\)
\(\Leftrightarrow AB=12.5\left(cm\right)\)
\(\Leftrightarrow AC=12.5\sqrt{3}\left(cm\right)\)
23 tháng 11 2023
a: Xét (O) có
CA,CM là tiếp tuyến
Do đó: CA=CM và OC là phân giác của \(\widehat{MOA}\)
=>\(\widehat{MOA}=2\cdot\widehat{MOC}\)
Xét (O) có
DM,DB là tiếp tuyến
Do đó: DM=DB và OD là phân giác của \(\widehat{MOB}\)
=>\(\widehat{MOB}=2\cdot\widehat{MOD}\)
\(\widehat{MOA}+\widehat{MOB}=180^0\)(hai góc kề bù)
=>\(2\cdot\widehat{MOD}+2\cdot\widehat{MOC}=180^0\)
=>\(2\cdot\left(\widehat{MOD}+\widehat{MOC}\right)=180^0\)
=>\(2\cdot\widehat{COD}=180^0\)
=>\(\widehat{COD}=90^0\)
=>ΔOCD vuông tại O
b: Xét ΔOCD vuông tại O có OM là đường cao
nên \(MC\cdot MD=OM^2=R^2\)
c: ΔOAC vuông tại A
=>\(OA^2+AC^2=OC^2\)
=>\(CA^2+R^2=\left(2R\right)^2=4R^2\)
=>\(CA^2=3R^2\)
=>\(CA=R\sqrt{3}\)
\(AC\cdot BD=MA\cdot MD=R^2\)
=>\(BD\cdot R\sqrt{3}=R^2\)
=>\(BD=\dfrac{R^2}{R\sqrt{3}}=\dfrac{R}{\sqrt{3}}\)
AH
Akai Haruma
Giáo viên
25 tháng 3 2021
Câu 4:
1. Hiển nhiên $AD\parallel BC$. Áp dụng định lý Talet:
$\frac{BM}{AN}=\frac{PM}{PN}$
$\frac{CM}{NE}=\frac{PM}{PN}$
$\Rightarrow \frac{BM}{AN}=\frac{CM}{NE}$. Mà $BM=CM$ do $M$ là trung điểm $BC$ nên $AN=NE$. $N$ thì nằm giữa $A,E$ (dễ cm)
Do đó $N$ là trung điểm $AE$
2.
Xét tam giác $ABC$ và $DCA$ có:
$\widehat{ABC}=\widehat{DCA}=90^0$
$\widehat{BCA}=\widehat{CAD}$ (so le trong)
$\Rightarrow \triangle ABC\sim \triangle DCA$ (g.g)
3. Theo định lý Pitago:
Từ tam giác đồng dạng phần 2 suy ra:
$\frac{AC}{DA}=\frac{BC}{CA}$
$\Rightarrow AD=\frac{AC^2}{BC}=\frac{6^2}{4}=9$ (cm)
4,Theo phần 1 thì:
$\frac{PM}{PN}=\frac{BM}{AN}=\frac{CM}{AN}$
Mà cũng theo định lý Talet: $\frac{CM}{AN}=\frac{QM}{QN}$
$\Rightarrow \frac{PM}{PN}=\frac{QM}{QN}$
(đpcm)
HT
3
7 tháng 10 2021
Câu 4:
\(x^6-1=\left(x^2-1\right)\left(x^4+x^2+1\right)⋮x^4+x^2+1\)