giúp mình với mình đag cần gấp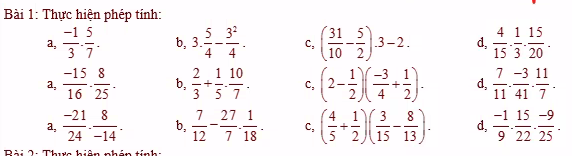
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1.
\(\sqrt{a}.\sqrt{\frac{32}{a}}=\sqrt{a.\frac{32}{a}}=\sqrt{32}=\sqrt{4^2.2}=4\sqrt{2}\)
2.
\(\sqrt{3,6a}.\sqrt{10a^3}=\sqrt{3,6a.10a^3}=\sqrt{36a^4}=\sqrt{(6a^2)^2}=6a^2\)
3.
\(\sqrt{0,5a}.\sqrt{50a^3}=\sqrt{0,5a.50a^3}=\sqrt{25a^4}=\sqrt{(5a^2)^2}=5a^2\)
4.
\(\sqrt{2a^3}.\sqrt{50a}=\sqrt{2a^3.50a}=\sqrt{100a^4}=\sqrt{(10a^2)^2}=10a^2\)

Em cần cụ thể bài nào thì nhờ mọi người nha, đừng up lên không nói gì như thế là không tôn trọng em ạ!


\(\dfrac{3^7.8^3}{6^5.12^2}=\dfrac{3^7.\left(2^3\right)^3}{\left(2.3\right)^5.\left(2^2.3\right)^2}=\dfrac{3^7.2^9}{2^5.3^5.2^4.3^2}=\dfrac{3^7.2^9}{3^7.2^9}=1\)
\(\dfrac{15^3+3.15^2+5^2.3^3}{7.5.3^3}=\dfrac{3^3.5^3+3.3^2.5^2+3^3.5^2}{7.5.3^3}=\dfrac{5.3^3\left(5^2+5+5\right)}{7.5.3^3}=\dfrac{25+5+5}{7}=5\)
c) \(\dfrac{3^7\cdot8^3}{6^5\cdot12^2}=\dfrac{3^7\cdot2^9}{2^5\cdot3^5\cdot3^2\cdot2^4}=1\)
d) \(\dfrac{15^3+3\cdot15^2+5^2\cdot3^3}{7\cdot5\cdot3^3}=\dfrac{15^3+3\cdot15^2+15^2\cdot3}{7\cdot5\cdot3^3}\)
\(=\dfrac{15^2\cdot\left(15+6\right)}{7\cdot5\cdot3^3}=\dfrac{3^3\cdot5^2\cdot7}{7\cdot5\cdot3^3}=5\)


a: Ta có: \(AN=NB=\dfrac{AB}{2}\)
\(AM=MC=\dfrac{AC}{2}\)
mà AB=AC
nên AN=NB=AM=MC
Xét ΔNBC và ΔMCB có
NB=MC
\(\widehat{NBC}=\widehat{MCB}\)(ΔABC cân tại A)
BC chung
Do đó: ΔNBC=ΔMCB
b: Xét ΔABC có
AD,BM,CN là các đường trung tuyến
AD,BM,CN đồng quy tại G
Do đó: G là trọng tâm của ΔABC
=>\(AG=2GD\)
mà AG=GE
nên GE=2GD
=>D là trung điểm của GE
=>DG=DE
c: Ta có: ΔABC cân tại A
mà AD là đường trung tuyến
nên AD\(\perp\)BC
Xét ΔCGE có
CD là đường cao
CD là đường trung tuyến
Do đó: ΔCGE cân tại C
d: Xét ΔABC có
BM là đường trung tuyến
G là trọng tâm
Do đó: \(BG=\dfrac{2}{3}BM=10\left(cm\right)\)
D là trung điểm của BC
=>DB=DC=BC/2=8(cm)
ΔGDB vuông tại D
=>\(GD^2+DB^2=GB^2\)
=>\(GD^2=10^2-8^2=36\)
=>\(GD=\sqrt{36}=6\left(cm\right)\)
\(\Leftrightarrow AG=2\cdot GD=12\left(cm\right)\)

1 replaced
2 freezed
3 applicants
4 priceless
5 breakage
6 suspiciously
7 suited
8 beheaded
9 residential
10 outrageous

Bài 2:
1.
$=(\frac{1}{7}+\frac{2}{7}+\frac{4}{7})+(\frac{3}{11}+\frac{8}{11})+2010$
$=\frac{7}{7}+\frac{11}{11}+2010=1+1+2010=2012$
2.
$=(\frac{2}{3}-\frac{2}{3})+(\frac{-3}{4}+\frac{3}{4})+(\frac{4}{5}-\frac{4}{5})+(\frac{-5}{6}+\frac{5}{6})+(\frac{6}{7}-\frac{6}{7})+(\frac{-7}{8}+\frac{7}{8})+\frac{1}{2012}$
$=0+0+0+0+0+0+\frac{1}{2012}=\frac{1}{2012}$
3.
$=\frac{1}{5-4}{4.5}+\frac{6-5}{5.6}+\frac{7-6}{6.7}+...+\frac{1}{20-19}{19.20}$
$=\frac{1}{4}-\frac{1}{5}+\frac{1}{5}-\frac{1}{6}+\frac{1}{6}-\frac{1}{7}+..+\frac{1}{19}-\frac{1}{20}$
$=\frac{1}{4}-\frac{1}{20}=\frac{1}{5}$
4.
\(=182\left[\frac{1+\frac{1}{5}-\frac{2}{7}+\frac{5}{13}}{2(1+\frac{1}{5}-\frac{2}{7}+\frac{5}{13})}: \frac{4(1-\frac{1}{33}-\frac{1}{57}+\frac{1}{7000})}{1-\frac{1}{33}-\frac{1}{57}+\frac{1}{7000}}\right]:\frac{10101\times 91}{10101\times 80}\)
$=182(\frac{1}{2}:4):\frac{91}{80}=182\times \frac{1}{8}\times \frac{80}{91}$
$=\frac{91\times 2\times 80}{8\times 91}=\frac{160}{8}=20$
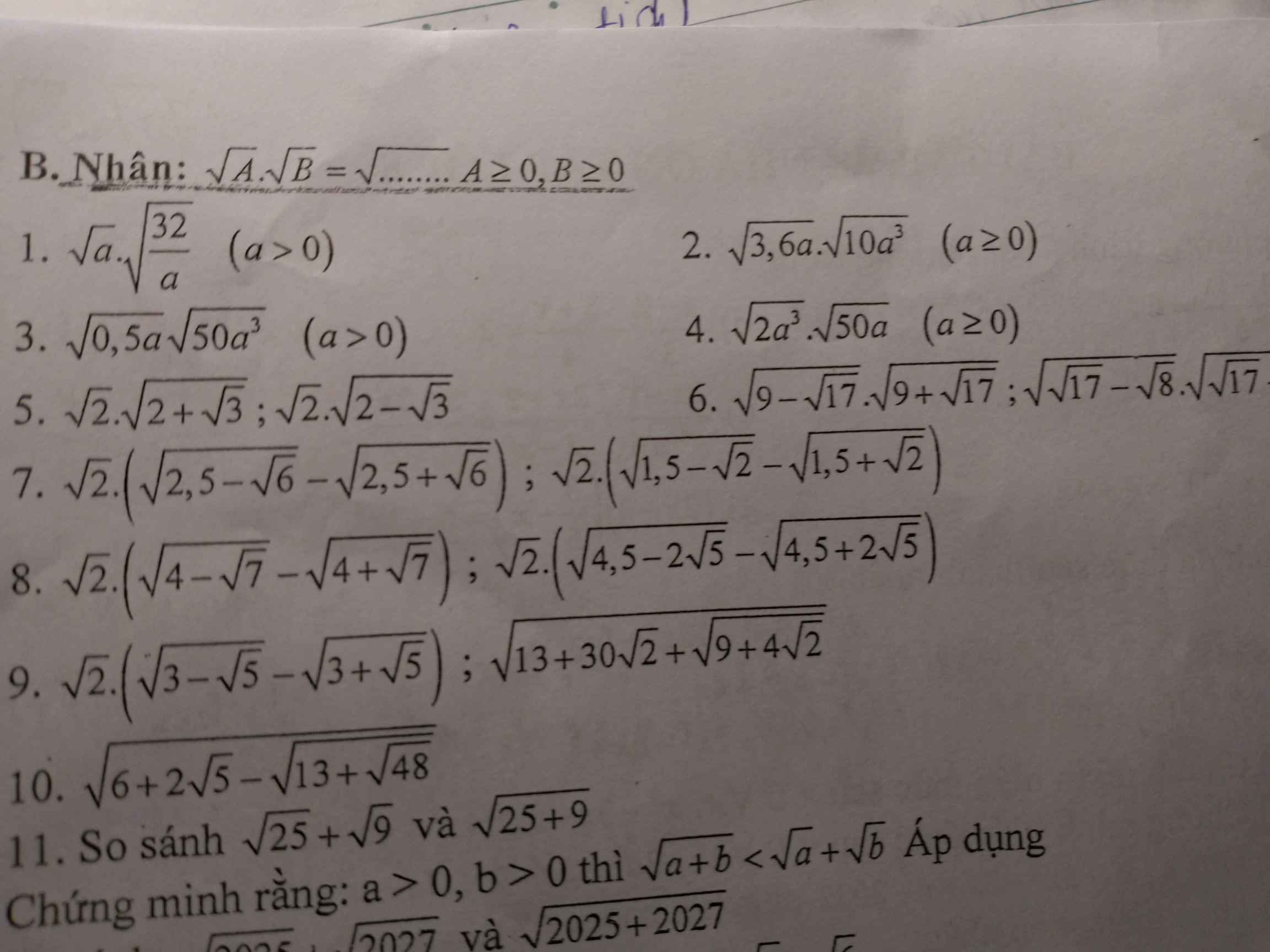




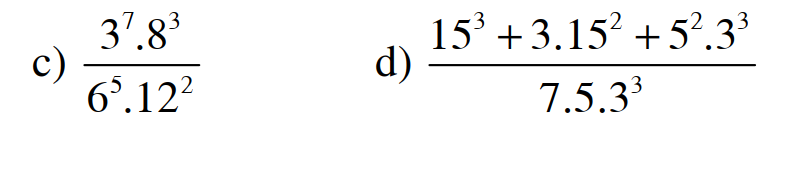



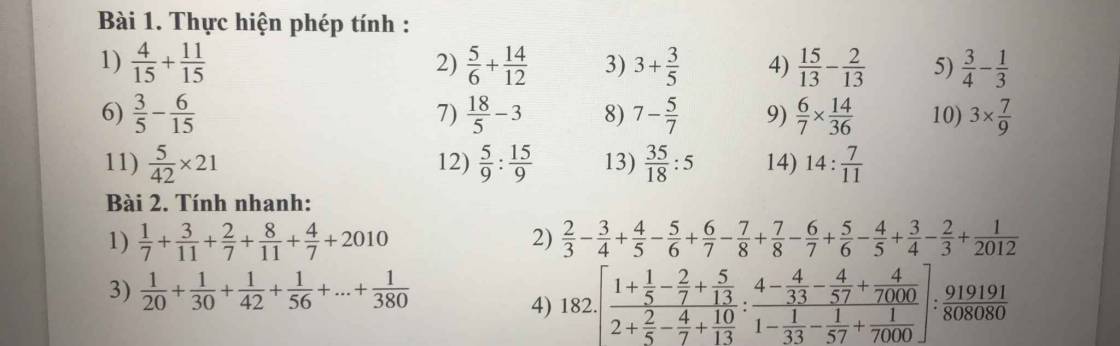
a: =-5/21
b: \(=\dfrac{15}{4}-\dfrac{9}{4}=\dfrac{6}{4}=\dfrac{3}{2}\)
c: \(=\left(\dfrac{31}{10}-\dfrac{25}{10}\right)\cdot3-2=\dfrac{6}{10}\cdot3-2=\dfrac{18}{10}-\dfrac{20}{10}=\dfrac{-2}{10}=\dfrac{-1}{5}\)
d: \(=\dfrac{4}{3}\cdot\dfrac{1}{20}=\dfrac{4}{60}=\dfrac{1}{15}\)
a: \(=\dfrac{-15}{25}\cdot\dfrac{8}{16}=\dfrac{-3}{5}\cdot\dfrac{1}{2}=\dfrac{-3}{10}\)
b: \(=\dfrac{2}{3}+\dfrac{2}{7}=\dfrac{20}{21}\)
c: \(=\dfrac{3}{2}\cdot\dfrac{-3+2}{4}=\dfrac{3}{2}\cdot\dfrac{-1}{4}=\dfrac{-3}{8}\)
d: \(=\dfrac{7}{11}\cdot\dfrac{11}{7}\cdot\dfrac{-3}{41}=-\dfrac{3}{41}\)