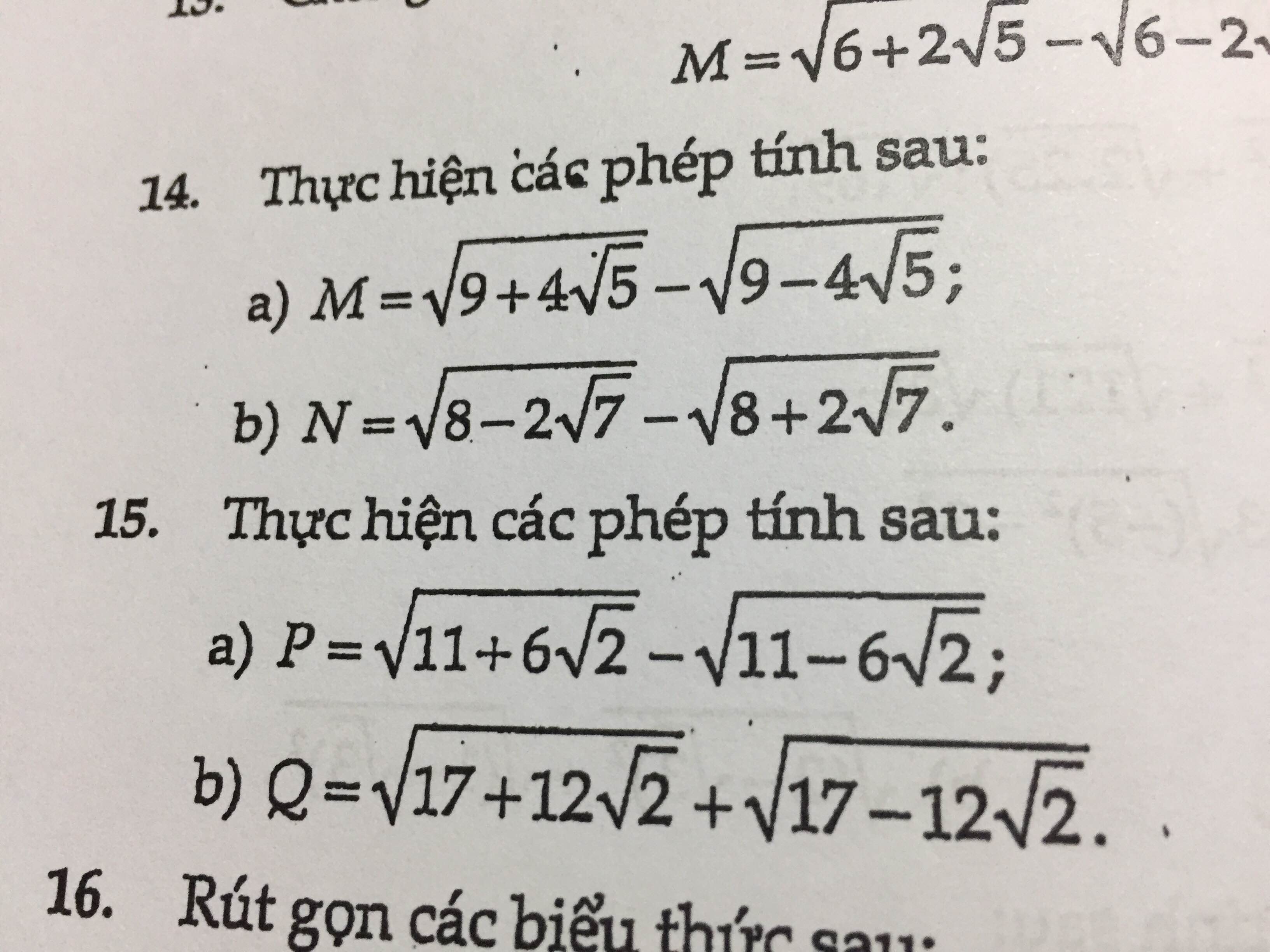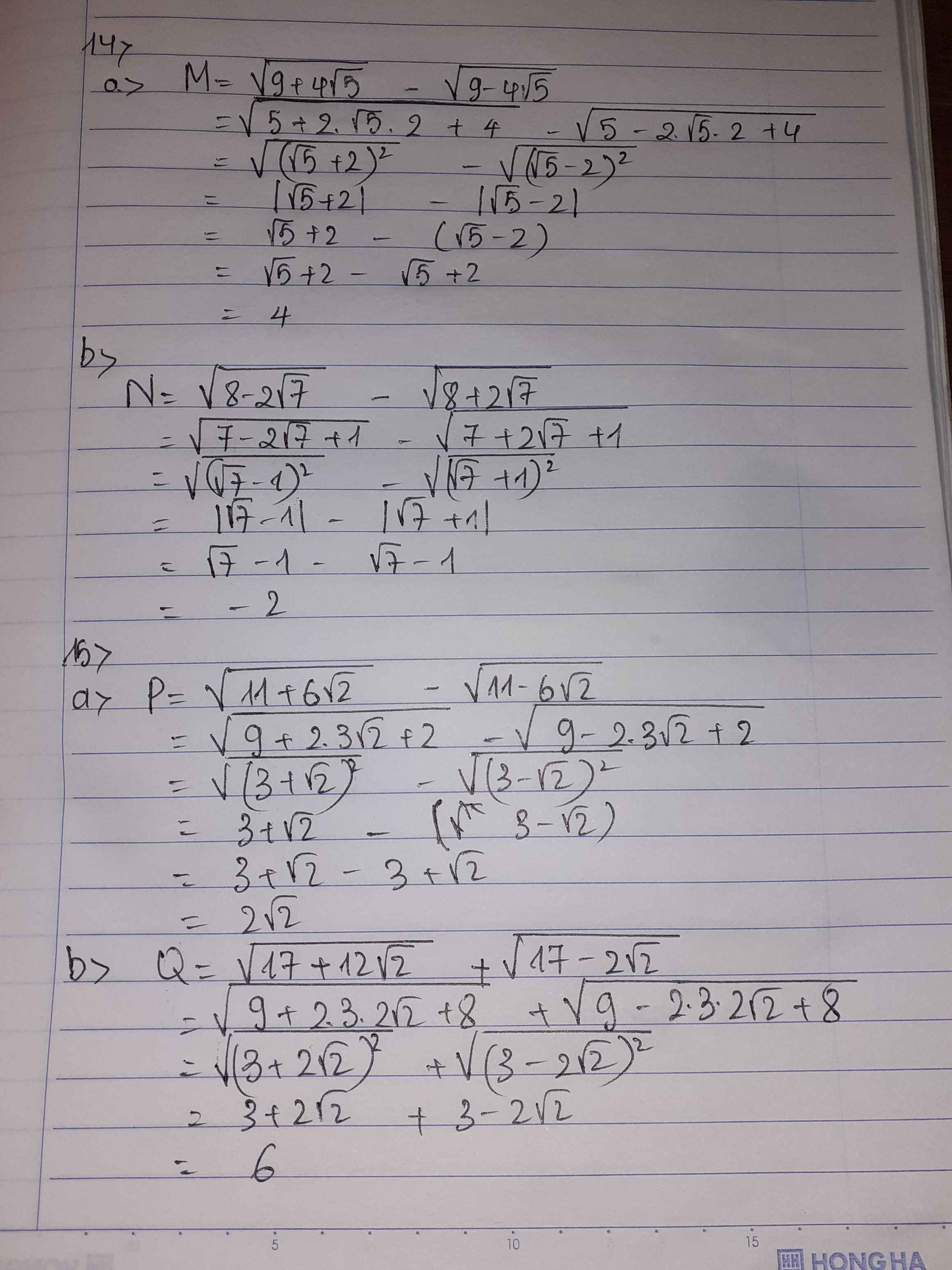Giải hộ mk bài 4 với
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
30 tháng 7 2021
Lời giải:
$(x+\frac{4}{9})^2\geq 0$ (do bình phương 1 số thì không âm)
$\frac{-49}{144}< 0$
Do đó: $(x+\frac{4}{9})^2> \frac{-49}{144}$ với mọi $x$ nên pt trên vô nghiệm.
31 tháng 7 2021
Ta có: \(\left(x+\dfrac{4}{9}\right)^2=-\dfrac{49}{144}\)
mà \(\left(x+\dfrac{4}{9}\right)^2\ge0\forall x\)
nên \(x\in\varnothing\)
MN
4
16 tháng 8 2021
a: Ta có: \(\dfrac{n\left(n+1\right)}{2}=231\)
\(\Leftrightarrow n^2+n-462=0\)
\(\Leftrightarrow n^2+22n-21n-462=0\)
\(\Leftrightarrow\left(n+22\right)\left(n-21\right)=0\)
\(\Leftrightarrow n=21\)
AD
5
AT
17 tháng 7 2021
14a) \(M=\sqrt{9+4\sqrt{5}}-\sqrt{9-4\sqrt{5}}\)
\(=\sqrt{\left(\sqrt{5}\right)^2+2.\sqrt{2}.2+2^2}-\sqrt{\left(\sqrt{5}\right)^2-2.\sqrt{2}.2+2^2}\)
\(=\sqrt{\left(\sqrt{5}+2\right)^2}-\sqrt{\left(\sqrt{5}-2\right)^2}=\left|\sqrt{5}+2\right|-\left|\sqrt{5}-2\right|\)
\(=\sqrt{5}+2-\sqrt{5}+2=4\)
b) \(N=\sqrt{8-2\sqrt{7}}-\sqrt{8+2\sqrt{7}}\)
\(=\sqrt{\left(\sqrt{7}\right)^2-2.\sqrt{7}.1+1^2}-\sqrt{\left(\sqrt{7}\right)^2+2.\sqrt{7}.1+1^2}\)
\(=\sqrt{\left(\sqrt{7}-1\right)^2}-\sqrt{\left(\sqrt{7}+1\right)^2}=\left|\sqrt{7}-1\right|-\left|\sqrt{7}+1\right|\)
\(=\sqrt{7}-1-\sqrt{7}-1=-2\)
15a) \(P=\sqrt{11+6\sqrt{2}}-\sqrt{11-6\sqrt{2}}\)
\(=\sqrt{3^2+2.3.\sqrt{2}+\left(\sqrt{2}\right)^2}-\sqrt{3^2-2.3.\sqrt{2}+\left(\sqrt{2}\right)^2}\)
\(=\sqrt{\left(3+\sqrt{2}\right)^2}-\sqrt{\left(3-\sqrt{2}\right)^2}=\left|3+\sqrt{2}\right|-\left|3-\sqrt{2}\right|\)
\(=3+\sqrt{2}-3+\sqrt{2}=2\sqrt{2}\)
b) \(Q=\sqrt{17+12\sqrt{2}}+\sqrt{17-12\sqrt{2}}\)
\(=\sqrt{3^2+2.3.2\sqrt{2}+\left(2\sqrt{2}\right)^2}+\sqrt{3^2-2.3.2\sqrt{2}+\left(2\sqrt{2}\right)^2}\)
\(=\sqrt{\left(3+2\sqrt{2}\right)^2}+\sqrt{\left(3-2\sqrt{2}\right)^2}=\left|3+2\sqrt{2}\right|+\left|3-2\sqrt{2}\right|\)
\(=3+2\sqrt{2}+3-2\sqrt{2}=6\)
MN
0
BK
1
TV
1
VD
21 tháng 3 2022
\(y-\dfrac{2}{3}=\dfrac{4}{5}\times\dfrac{3}{4}\\ y-\dfrac{2}{3}=\dfrac{3}{5}\\ y=\dfrac{3}{5}+\dfrac{2}{3}\\ y=\dfrac{9}{15}+\dfrac{10}{15}\\ y=\dfrac{19}{15}\)
2 tháng 8 2021
Câu 3:
a) Ta có: \(x^2-1=3\)
\(\Leftrightarrow x^2=4\)
hay \(x\in\left\{2;-2\right\}\)
b) Ta có: \(\sqrt{16x}-2\sqrt{36x}+\sqrt{9x}=2\)
\(\Leftrightarrow4\sqrt{x}-12\sqrt{x}+3\sqrt{x}=2\)
\(\Leftrightarrow-5\sqrt{x}=2\)(Vô lý)